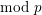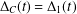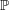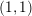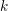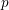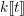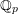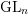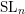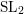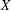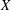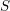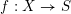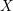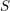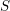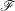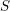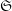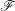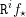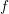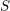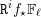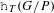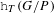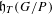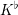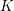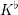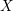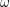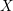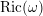Refine listing
Actions for selected content:
381 results in 14Fxx
SUR LA PRÉSERVATION DE LA COHÉRENCE PAR IMAGE INVERSE EXTRAORDINAIRE D’UNE IMMERSION FERMÉE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 14 June 2019, pp. 125-170
-
- Article
-
- You have access
- HTML
- Export citation
REFINED SWAN CONDUCTORS
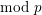 $\text{mod}~p$ OF ONE-DIMENSIONAL GALOIS REPRESENTATIONS
$\text{mod}~p$ OF ONE-DIMENSIONAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 03 June 2019, pp. 134-182
-
- Article
-
- You have access
- HTML
- Export citation
ON COMPLEX HOMOGENEOUS SINGULARITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 27 May 2019, pp. 395-409
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
IRREGULAR HODGE FILTRATION OF SOME CONFLUENT HYPERGEOMETRIC SYSTEMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 24 May 2019, pp. 627-668
- Print publication:
- March 2021
-
- Article
- Export citation
CONSTANCY OF NEWTON POLYGONS OF
 $F$-ISOCRYSTALS ON ABELIAN VARIETIES AND ISOTRIVIALITY OF FAMILIES OF CURVES
$F$-ISOCRYSTALS ON ABELIAN VARIETIES AND ISOTRIVIALITY OF FAMILIES OF CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 14 May 2019, pp. 587-625
- Print publication:
- March 2021
-
- Article
- Export citation
Formality of
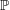 $\mathbb{P}$-objects
$\mathbb{P}$-objects
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 03 May 2019, pp. 973-994
- Print publication:
- May 2019
-
- Article
- Export citation
Cycle classes in overconvergent rigid cohomology and a semistable Lefschetz
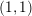 $(1,1)$ theorem
$(1,1)$ theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 02 May 2019, pp. 1025-1045
- Print publication:
- May 2019
-
- Article
- Export citation
Autoequivalences of twisted K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 30 April 2019, pp. 912-937
- Print publication:
- May 2019
-
- Article
- Export citation
MOTIVIC EULER CHARACTERISTICS AND WITT-VALUED CHARACTERISTIC CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 22 March 2019, pp. 251-310
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OBSTRUCTIONS TO ALGEBRAIZING TOPOLOGICAL VECTOR BUNDLES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 21 March 2019, e6
-
- Article
-
- You have access
- Open access
- Export citation
Constructibilité et modération uniformes en cohomologie étale
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 19 March 2019, pp. 711-757
- Print publication:
- April 2019
-
- Article
- Export citation
Grothendieck Ring of Varieties with Actions of Finite Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 08 March 2019, pp. 925-948
-
- Article
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
- Print publication:
- November 2020
-
- Article
- Export citation
On two cohomological Hall algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1581-1607
- Print publication:
- June 2020
-
- Article
- Export citation
Mixed Perverse Sheaves on Flag Varieties for Coxeter Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1-55
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
HASSE PRINCIPLES FOR ÉTALE MOTIVIC COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 63-83
-
- Article
-
- You have access
- HTML
- Export citation
DUALITY FOR COHOMOLOGY OF CURVES WITH COEFFICIENTS IN ABELIAN VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 42-149
-
- Article
-
- You have access
- HTML
- Export citation
ZERO-LOCI OF BRAUER GROUP ELEMENTS ON SEMI-SIMPLE ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1467-1507
- Print publication:
- September 2020
-
- Article
- Export citation
A motivic version of the theorem of Fontaine and Wintenberger
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 38-88
- Print publication:
- January 2019
-
- Article
- Export citation
A partial converse to the Andreotti–Grauert theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 19 November 2018, pp. 89-99
- Print publication:
- January 2019
-
- Article
- Export citation