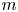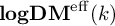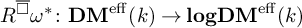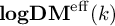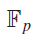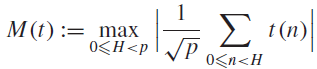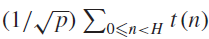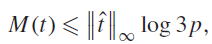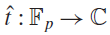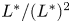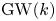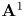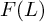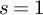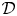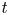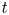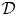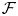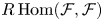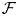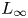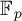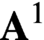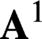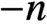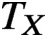Refine listing
Actions for selected content:
378 results in 14Fxx
EULER CLASSES: SIX-FUNCTORS FORMALISM, DUALITIES, INTEGRALITY AND LINEAR SUBSPACES OF COMPLETE INTERSECTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 16 July 2021, pp. 681-746
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The cohomology rings of real toric spaces and smooth real toric varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 720-737
- Print publication:
- June 2022
-
- Article
- Export citation
The distribution of the maximum of partial sums of Kloosterman sums and other trace functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 28 June 2021, pp. 1610-1651
- Print publication:
- July 2021
-
- Article
- Export citation
Counterexamples to Hochschild-Kostant-Rosenberg in characteristic p
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 22 June 2021, e49
-
- Article
-
- You have access
- Open access
- Export citation
CONNECTIVITY AND PURITY FOR LOGARITHMIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 14 June 2021, pp. 335-381
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
K-theory of valuation rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 20 May 2021, pp. 1121-1142
- Print publication:
- June 2021
-
- Article
- Export citation
STEENROD OPERATIONS ON THE DE RHAM COHOMOLOGY OF ALGEBRAIC STACKS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 May 2021, pp. 493-540
- Print publication:
- March 2023
-
- Article
- Export citation
On the size of the maximum of incomplete Kloosterman sums
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 15 April 2021, pp. 563-590
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
An arithmetic count of the lines on a smooth cubic surface
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 08 April 2021, pp. 677-709
- Print publication:
- April 2021
-
- Article
- Export citation
RECIPROCITY SHEAVES AND THEIR RAMIFICATION FILTRATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 19 March 2021, pp. 71-144
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
SPECIAL VALUES OF THE ZETA FUNCTION OF AN ARITHMETIC SURFACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 March 2021, pp. 2043-2091
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Irregular perverse sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 573-624
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Formality conjecture for minimal surfaces of Kodaira dimension 0
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 February 2021, pp. 215-235
- Print publication:
- February 2021
-
- Article
- Export citation
Log
 $\mathscr{D}$-modules and index theorems
$\mathscr{D}$-modules and index theorems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e3
-
- Article
-
- You have access
- Open access
- Export citation
ATIYAH CLASS AND CHERN CHARACTER FOR GLOBAL MATRIX FACTORISATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1445-1470
- Print publication:
- July 2022
-
- Article
- Export citation
The categorified Grothendieck–Riemann–Roch theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 154-214
- Print publication:
- January 2021
-
- Article
- Export citation
The localization theorem for framed motivic spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 February 2021, pp. 1-11
- Print publication:
- January 2021
-
- Article
- Export citation
ISOTROPIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 22 December 2020, pp. 1271-1330
- Print publication:
- July 2022
-
- Article
- Export citation
Modules over algebraic cobordism
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 17 December 2020, e14
-
- Article
-
- You have access
- Open access
- Export citation
RC-positive metrics on rationally connected manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 16 November 2020, e53
-
- Article
-
- You have access
- Open access
- Export citation