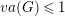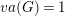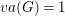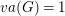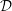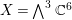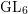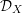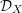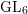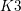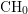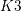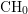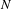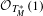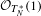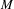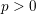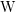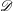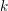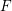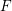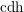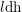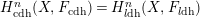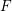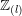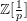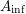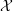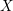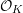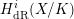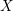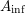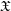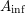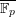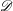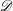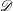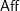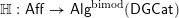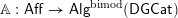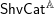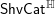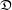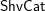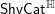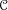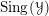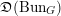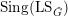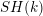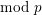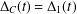Refine listing
Actions for selected content:
378 results in 14Fxx
THE UNIT MAP OF THE ALGEBRAIC SPECIAL LINEAR COBORDISM SPECTRUM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 24 December 2019, pp. 1905-1930
- Print publication:
- November 2021
-
- Article
- Export citation
VIRTUAL ALGEBRAIC FIBRATIONS OF KÄHLER GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 42-60
- Print publication:
- September 2021
-
- Article
- Export citation
EQUIVARIANT
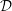 ${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 29 November 2019, pp. 61-82
- Print publication:
- September 2021
-
- Article
- Export citation
Derived categories of
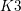 $K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
$K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 179-197
- Print publication:
- January 2020
-
- Article
- Export citation
ALGEBRAIC ISOMONODROMIC DEFORMATIONS AND THE MAPPING CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 1497-1545
- Print publication:
- September 2021
-
- Article
- Export citation
Relative Equivariant Motives and Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 08 November 2019, pp. 131-159
- Print publication:
- February 2021
-
- Article
- Export citation
Compatible systems and ramification
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 21 October 2019, pp. 2334-2353
- Print publication:
- December 2019
-
- Article
- Export citation
RC-POSITIVITY, VANISHING THEOREMS AND RIGIDITY OF HOLOMORPHIC MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 11 October 2019, pp. 1023-1038
- Print publication:
- May 2021
-
- Article
- Export citation
On higher direct images of convergent isocrystals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 25 September 2019, pp. 2180-2213
- Print publication:
- November 2019
-
- Article
- Export citation
THE GAMMA CONSTRUCTION AND ASYMPTOTIC INVARIANTS OF LINE BUNDLES OVER ARBITRARY FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 23 September 2019, pp. 165-207
- Print publication:
- June 2021
-
- Article
- Export citation
A BETTER COMPARISON OF
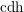 $\operatorname{cdh}$- AND
$\operatorname{cdh}$- AND 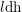 $l\operatorname{dh}$-COHOMOLOGIES
$l\operatorname{dh}$-COHOMOLOGIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 13 September 2019, pp. 183-213
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
The
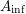 $A_{\text{inf}}$-cohomology in the semistable case
$A_{\text{inf}}$-cohomology in the semistable case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 09 September 2019, pp. 2039-2128
- Print publication:
- November 2019
-
- Article
- Export citation
tt-geometry of Tate motives over algebraically closed fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 06 September 2019, pp. 1888-1923
- Print publication:
- October 2019
-
- Article
- Export citation
Nearly free curves and arrangements: a vector bundle point of view
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 51-74
- Print publication:
- January 2021
-
- Article
- Export citation
AROUND THE NEARBY CYCLE FUNCTOR FOR ARITHMETIC
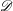 $\mathscr{D}$-MODULES
$\mathscr{D}$-MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 28 August 2019, pp. 1-28
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
Sheaves of categories with local actions of Hochschild cochains
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1521-1567
- Print publication:
- August 2019
-
- Article
- Export citation
Reconstructing rational stable motivic homotopy theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1424-1443
- Print publication:
- July 2019
-
- Article
- Export citation
SUR LA PRÉSERVATION DE LA COHÉRENCE PAR IMAGE INVERSE EXTRAORDINAIRE D’UNE IMMERSION FERMÉE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 14 June 2019, pp. 125-170
- Print publication:
- March 2021
-
- Article
- Export citation
REFINED SWAN CONDUCTORS
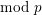 $\text{mod}~p$ OF ONE-DIMENSIONAL GALOIS REPRESENTATIONS
$\text{mod}~p$ OF ONE-DIMENSIONAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 03 June 2019, pp. 134-182
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
ON COMPLEX HOMOGENEOUS SINGULARITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 27 May 2019, pp. 395-409
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation