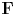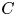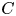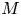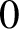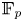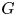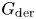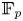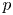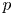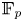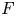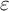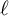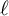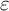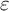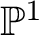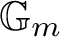Refine listing
Actions for selected content:
378 results in 14Fxx
Categorical traces and a relative Lefschetz–Verdier formula
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 07 February 2022, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The monodromy of unit-root F-isocrystals with geometric origin
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 18 April 2022, pp. 334-365
- Print publication:
- February 2022
-
- Article
- Export citation
The six functors for Zariski-constructible sheaves in rigid geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 437-482
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological models for stable motivic invariants of regular number rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 January 2022, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dieudonné theory via cohomology of classifying stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 December 2021, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum to ‘Endoscopy for Hecke categories, character sheaves and representations’
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 30 November 2021, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE TOM DIECK SPLITTING THEOREM IN EQUIVARIANT MOTIVIC HOMOTOPY THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1181-1250
- Print publication:
- May 2023
-
- Article
- Export citation
Cohomological invariants of root stacks and admissible double coverings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 November 2021, pp. 202-224
- Print publication:
- February 2023
-
- Article
- Export citation
Free quotients of fundamental groups of smooth quasi-projective varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 27 October 2021, pp. 924-946
-
- Article
- Export citation
A homotopy exact sequence for overconvergent isocrystals
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 25 October 2021, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Period sheaves via derived de Rham cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2021, pp. 2377-2406
- Print publication:
- November 2021
-
- Article
- Export citation
Brauer groups of moduli of hyperelliptic curves via cohomological invariants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 17 September 2021, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central elements in affine mod p Hecke algebras via perverse
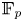 $\mathbb {F}_p$-sheaves
$\mathbb {F}_p$-sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2215-2241
- Print publication:
- October 2021
-
- Article
- Export citation
A generalization of the b-function lemma
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 07 September 2021, pp. 2199-2214
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GEOMETRIC LOCAL
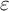 $\varepsilon $-FACTORS IN HIGHER DIMENSIONS
$\varepsilon $-FACTORS IN HIGHER DIMENSIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 September 2021, pp. 1887-1913
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Computing the fundamental group of a higher-rank graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 26 August 2021, pp. 650-661
-
- Article
- Export citation
LOGARITHMIC DE RHAM–WITT COMPLEXES VIA THE DÉCALAGE OPERATOR
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 26 August 2021, pp. 1319-1382
- Print publication:
- May 2023
-
- Article
- Export citation
De Rham–Witt sheaves via algebraic cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 2089-2132
- Print publication:
- October 2021
-
- Article
- Export citation
THE ZEROTH
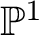 $\mathbb P^1$-STABLE HOMOTOPY SHEAF OF A MOTIVIC SPACE
$\mathbb P^1$-STABLE HOMOTOPY SHEAF OF A MOTIVIC SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1293-1317
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPARISON OF KUMMER LOGARITHMIC TOPOLOGIES WITH CLASSICAL TOPOLOGIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 27 July 2021, pp. 1087-1117
- Print publication:
- May 2023
-
- Article
- Export citation