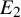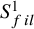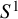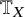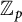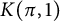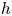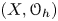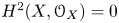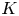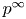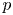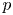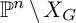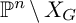Refine listing
Actions for selected content:
378 results in 14Fxx
Hyperplane Arrangements Satisfy (Un)Twisted Logarithmic Comparison Theorems, Applications to
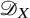 $\mathscr {D}_{X}$-modules
$\mathscr {D}_{X}$-modules
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Syntomic cycle classes and prismatic Poincaré duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 07 October 2024, pp. 2322-2365
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lefschetz theorems in flat cohomology and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1850-1870
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the integral part of A-motivic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 1715-1783
- Print publication:
- August 2024
-
- Article
- Export citation
Singer conjecture for varieties with semismall Albanese map and residually finite fundamental group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-7
-
- Article
- Export citation
Completed prismatic F-crystals and crystalline Zp-local systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1101-1166
- Print publication:
- May 2024
-
- Article
- Export citation
Cohomological Descent for Faltings Ringed Topos
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on Hodge–Tate spectral sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 22 March 2024, pp. 625-642
- Print publication:
- May 2024
-
- Article
-
- You have access
- HTML
- Export citation
Models and integral differentials of hyperelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 18 March 2024, pp. 382-439
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral equivariant cohomology of affine Grassmannians
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 727-741
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cogroupoid structures on the circle and the Hodge degeneration
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 January 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Faltings’ main p-adic comparison theorems for non-smooth schemes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 12 January 2024, pp. 426-458
- Print publication:
- April 2025
-
- Article
- Export citation
On the Bezrukavnikov–Kaledin quantization of symplectic varieties in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 411-450
- Print publication:
- February 2024
-
- Article
- Export citation
The Grothendieck–Serre conjecture over valuation rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 317-355
- Print publication:
- February 2024
-
- Article
- Export citation
Boundedness of the p-primary torsion of the Brauer group of an abelian variety
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 463-480
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A COMPARISON BETWEEN DWORK AND RIGID COHOMOLOGIES OF PROJECTIVE COMPLEMENTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 420-461
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Drinfeld's lemma for F-isocrystals, II: Tannakian approach
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 90-119
- Print publication:
- January 2024
-
- Article
- Export citation
The tamely ramified geometric quantitative minimal ramification problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 21-51
- Print publication:
- January 2024
-
- Article
- Export citation
ON ENDOMORPHISMS OF EXTENSIONS IN TANNAKIAN CATEGORIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 07 November 2023, pp. 103-114
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Notes on hyperelliptic mapping class groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 126-161
- Print publication:
- January 2024
-
- Article
- Export citation
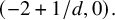
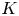
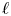
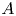

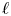
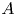
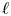
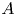
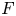
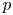
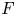
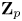
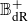
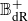
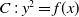
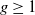
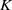
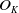
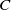
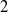
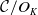
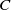
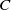
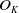
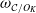
 .
.