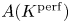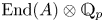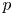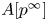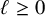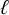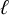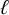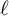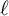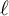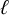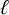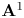Refine listing
Actions for selected content:
378 results in 14Fxx
NON-ISOMORPHIC SMOOTH COMPACTIFICATIONS OF THE MODULI SPACE OF CUBIC SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 03 October 2023, pp. 315-365
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On distributivity in higher algebra I: the universal property of bispans
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 2326-2415
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perfect points of abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. 2261-2278
- Print publication:
- November 2023
-
- Article
- Export citation
ODD RANK VECTOR BUNDLES IN ETA-PERIODIC MOTIVIC HOMOTOPY THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1733-1764
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the u∞-torsion submodule of prismatic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 1607-1672
- Print publication:
- August 2023
-
- Article
- Export citation
Weight filtrations on Selmer schemes and the effective Chabauty–Kim method
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1531-1605
- Print publication:
- July 2023
-
- Article
- Export citation
Weighted Hodge ideals of reduced divisors
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 June 2023, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Refined unramified cohomology of schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1466-1530
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative regular Riemann–Hilbert correspondence II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1413-1465
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A BERNSTEIN–SATO POLYNOMIAL OF A MEROMORPHIC FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 06 June 2023, pp. 715-733
- Print publication:
- September 2023
-
- Article
- Export citation
Efficient simplicial replacement of semialgebraic sets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 May 2023, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Groups of symplectic involutions on symplectic varieties of Kummer type and their fixed loci
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 May 2023, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of Log Terminal and Semi Log Canonical Singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 May 2023, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local terms for transversal intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 985-1004
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
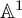 ${\mathbb A}^1$-CONNECTEDNESS OF MODULI OF VECTOR BUNDLES ON A CURVE
${\mathbb A}^1$-CONNECTEDNESS OF MODULI OF VECTOR BUNDLES ON A CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 1019-1027
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNIFORM LOCAL CONSTANCY OF ÉTALE COHOMOLOGY OF RIGID ANALYTIC VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 28 February 2023, pp. 839-896
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noninjectivity of the cycle class map in continuous
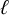 $\ell $-adic cohomology
$\ell $-adic cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 February 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reciprocity sheaves and logarithmic motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. 355-379
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prismatic Dieudonné Theory
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 January 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Syntomic complexes and p-adic étale Tate twists
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 January 2023, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation