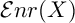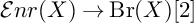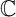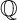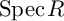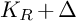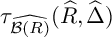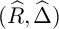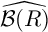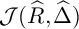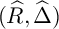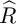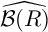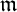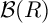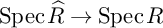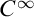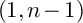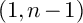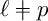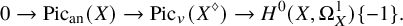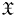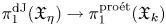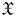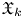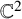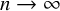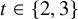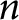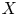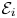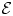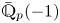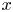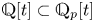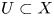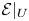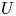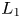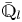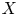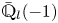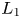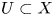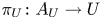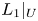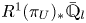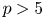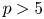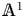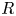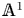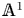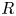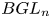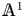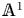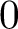Refine listing
Actions for selected content:
378 results in 14Fxx
ENRIQUES INVOLUTIONS AND BRAUER CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 606-621
- Print publication:
- September 2023
-
- Article
- Export citation
BIG COHEN–MACAULAY TEST IDEALS IN EQUAL CHARACTERISTIC ZERO VIA ULTRAPRODUCTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 07 December 2022, pp. 549-575
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
O-minimal de Rham Cohomology
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 16 January 2023, p. 529
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
COHOMOLOGY OF THE BRUHAT–TITS STRATA IN THE UNRAMIFIED UNITARY RAPOPORT–ZINK SPACE OF SIGNATURE
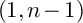 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 470-497
- Print publication:
- June 2023
-
- Article
- Export citation
Non-abelian Mellin transformations and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 November 2022, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Absolute Poincaré duality in étale cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 November 2022, e99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hodge filtration on local cohomology, Du Bois complex and local cohomological dimension
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 03 October 2022, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PONTRYAGIN DUALITY FOR VARIETIES OVER p-ADIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2022, pp. 425-462
- Print publication:
- January 2024
-
- Article
- Export citation
LAURICELLA HYPERGEOMETRIC FUNCTIONS, UNIPOTENT FUNDAMENTAL GROUPS OF THE PUNCTURED RIEMANN SPHERE, AND THEIR MOTIVIC COACTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 148-220
- Print publication:
- March 2023
-
- Article
- Export citation
Line bundles on rigid spaces in the v-topology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 22 September 2022, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the cohomology of reciprocity sheaves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 30 August 2022, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The six-functor formalism for rigid analytic motives
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 August 2022, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Specialization for the pro-étale fundamental group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 27 September 2022, pp. 1713-1745
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distributions on partitions arising from Hilbert schemes and hook lengths
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 29 June 2022, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting Betti distributions of Hilbert schemes on n points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 May 2022, pp. 243-258
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hecke action on the principal block
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 19 July 2022, pp. 953-1019
- Print publication:
- May 2022
-
- Article
- Export citation
Rank 2 local systems and abelian varieties II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 868-892
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Kawamata–Viehweg vanishing theorem for log del Pezzo surfaces in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 750-763
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Localization and nilpotent spaces in
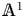 ${\mathbb {A}}^1$-homotopy theory
${\mathbb {A}}^1$-homotopy theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 27 May 2022, pp. 654-720
- Print publication:
- March 2022
-
- Article
- Export citation
ZERO-CYCLES ON NORMAL PROJECTIVE VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 2241-2295
- Print publication:
- September 2023
-
- Article
- Export citation