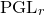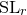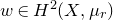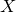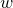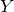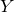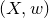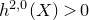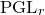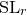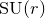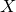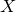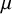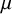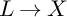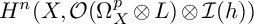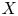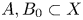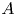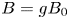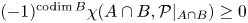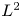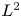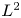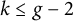Refine listing
Actions for selected content:
378 results in 14Fxx
A virtual
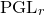 ${\rm PGL}_r$–
${\rm PGL}_r$–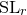 ${\rm SL}_r$ correspondence for projective surfaces
${\rm SL}_r$ correspondence for projective surfaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bernstein–Sato polynomials of locally quasi-homogeneous divisors in
 $\mathbb{C}^{3}$
$\mathbb{C}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 859-915
- Print publication:
- April 2025
-
- Article
- Export citation
Deformation theory for prismatic G-displays
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 March 2025, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The birational geometry of moduli of cubic surfaces and cubic surfaces with a line
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NON-ARCHIMEDEAN MONGE–AMPÈRE EQUATION IN MIXED CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 04 March 2025, pp. 548-561
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric local systems on the projective line minus four points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 01 July 2025, pp. 536-554
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRIANGULATED CHARACTERIZATIONS OF SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 24 February 2025, e3
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME RESULTS ON THE TOPOLOGY OF ALGEBRAIC SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 376-397
- Print publication:
- June 2025
-
- Article
- Export citation
p-adic Simpson correspondences for principal bundles in abelian settings
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSION OF COHOMOLOGY CLASSES FOR VECTOR BUNDLES WITH SINGULAR HERMITIAN METRICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 562-580
- Print publication:
- September 2025
-
- Article
- Export citation
Prismatic Dieudonné Theory – ERRATUM
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
“The six-functor formalism for rigid analytic motives” – Erratum
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 February 2025, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A BOGOMOLOV TYPE VANISHING THEOREM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 170-182
- Print publication:
- March 2025
-
- Article
- Export citation
A new generic vanishing theorem on homogeneous varieties and the positivity conjecture for triple intersections of Schubert cells
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-12
- Print publication:
- January 2025
-
- Article
- Export citation
A power structure over the Grothendieck ring of geometric dg categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 05 December 2024, pp. 300-318
-
- Article
- Export citation
Vanishing theorem for tame harmonic bundles via L2-cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 03 April 2025, pp. 2828-2855
- Print publication:
- December 2024
-
- Article
- Export citation
Cohomological boundedness for flat bundles on surfaces and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 20 February 2025, pp. 2775-2827
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DUAL NAKANO POSITIVITY AND SINGULAR NAKANO POSITIVITY OF DIRECT IMAGE SHEAVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 55-78
- Print publication:
- March 2025
-
- Article
- Export citation
Non-torsion algebraic cycles on the Jacobians of Fermat quotients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 60-72
- Print publication:
- March 2025
-
- Article
- Export citation
AN EXAMPLE OF THE JANTZEN FILTRATION OF A D-MODULE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 265-296
- Print publication:
- June 2025
-
- Article
- Export citation