Refine listing
Actions for selected content:
300 results in 14Hxx
Numerical criteria for divisors on
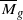 to be ample
to be ample
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 04 September 2009, pp. 1227-1248
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Harmonic and equianharmonic equations in the Grothendieck–Teichmüller group. III
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 431-448
- Print publication:
- April 2010
-
- Article
- Export citation
τ-function of discrete isomonodromy transformations and probability
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 747-772
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
VECTOR BUNDLES OVER A NONDEGENERATE CONIC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 145-154
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
ON THE INTERSECTION OF RATIONAL TRANSVERSAL SUBTORI
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 221-231
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
On the independence of the generators of tautological rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1497-1503
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
Towards an enumerative geometry of the moduli space of twisted curvesand rth roots
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1461-1496
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
FROBENIUS GROUPS AS MONODROMY GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 191-196
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Oort groups and lifting problems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 849-866
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
Deformation of finite morphisms and smoothing of ropes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 673-688
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Petri map for rank two bundles with canonical determinant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 705-720
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Moduli spaces of orthogonal and symplectic bundles over an algebraic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 721-733
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Geometric Waldspurger periods
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 377-438
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The arithmetic of Prym varieties in genus 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 317-338
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Linear series and the existence of branched covers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 89-106
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
On the Quadratic Twists of a Family of Elliptic Curves
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 139-154
- Print publication:
- December 2005
-
- Article
- Export citation
Integral points on elliptic curves over function fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 197-208
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
On real forms of a complex algebraic curve
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-142
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
The characterization of elliptic curves over finite fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 275-286
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
Weierstrass equations and the minimal discriminant of an elliptic curve
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 245-251
- Print publication:
- December 1984
-
- Article
- Export citation
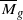 to be ample
to be ample
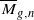 of
of 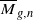
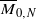 for
for 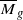 is known to be of general type.
is known to be of general type.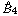 . A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.
. A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.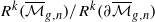 for all
for all 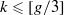 . We also give a simple argument for
. We also give a simple argument for 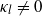 in
in  .
.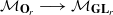 (respectively
(respectively 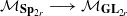 ) from the moduli space of orthogonal (respectively symplectic) bundles to the moduli space of all vector bundles over
) from the moduli space of orthogonal (respectively symplectic) bundles to the moduli space of all vector bundles over 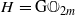 ,
, 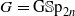 over
over 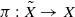 . Let
. Let 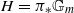 with
with 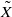 connected. We establish the geometric Langlands functoriality for this pair. Namely, we show that
connected. We establish the geometric Langlands functoriality for this pair. Namely, we show that 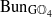 to
to 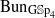 . Based on these calculations, we give three conjectural constructions of certain automorphic sheaves on
. Based on these calculations, we give three conjectural constructions of certain automorphic sheaves on 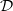 -modules only).
-modules only).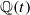 . By specialization, this also gives examples over
. By specialization, this also gives examples over 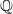 .
.