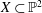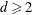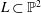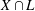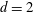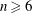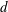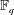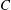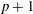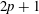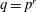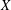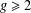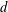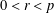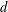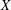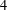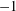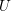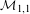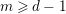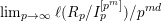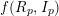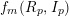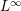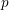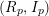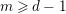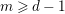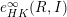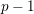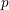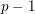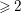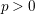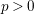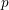Refine listing
Actions for selected content:
300 results in 14Hxx
On a Property of Real Plane Curves of Even Degree
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 179-182
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Sharp Bertini Theorem for Plane Curves over Finite Fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 223-230
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Galois theory for general systems of polynomial equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 229-245
- Print publication:
- February 2019
-
- Article
- Export citation
ON MAXIMALLY FROBENIUS DESTABILISED VECTOR BUNDLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 195-202
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Dynamical degrees of Hurwitz correspondences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1968-1990
- Print publication:
- July 2020
-
- Article
- Export citation
FUJITA DECOMPOSITION AND HODGE LOCI
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 12 November 2018, pp. 1389-1408
- Print publication:
- July 2020
-
- Article
- Export citation
MOTIVIC HILBERT ZETA FUNCTIONS OF CURVES ARE RATIONAL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 31 October 2018, pp. 947-964
- Print publication:
- May 2020
-
- Article
- Export citation
Smoothing of Limit Linear Series on Curves and Metrized Complexes of Pseudocompact Type
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 16 October 2018, pp. 629-658
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
BETTI NUMBERS FOR CERTAIN COHEN–MACAULAY TANGENT CONES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 68-77
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
SINGULARITIES OF THE BIEXTENSION METRIC FOR FAMILIES OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 July 2018, e12
-
- Article
-
- You have access
- Open access
- Export citation
On a purely inseparable analogue ofthe Abhyankar conjecture for affine curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 1633-1658
- Print publication:
- August 2018
-
- Article
- Export citation
HIGGS BUNDLES OVER ELLIPTIC CURVES FOR COMPLEX REDUCTIVE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 16 July 2018, pp. 297-320
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
Model Completeness for the Real Field with the Weierstrass ℘ Function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 811-823
-
- Article
- Export citation
UNIVERSAL MIXED ELLIPTIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 30 April 2018, pp. 663-766
- Print publication:
- May 2020
-
- Article
- Export citation
TOWARD HILBERT–KUNZ DENSITY FUNCTIONSIN CHARACTERISTIC 0
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 08 March 2018, pp. 158-200
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
ALEXANDER POLYNOMIALS OF COMPLEX PROJECTIVE PLANE CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 March 2018, pp. 386-395
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
A NOTE ON DORMANT OPERS OF RANK
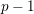 $p-1$ IN CHARACTERISTIC
$p-1$ IN CHARACTERISTIC 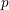 $p$
$p$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 19 February 2018, pp. 115-126
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
Some Remarks on the Wiman–Edge Pencil
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 401-412
-
- Article
-
- You have access
- Export citation
Birational invariance in logarithmicGromov–Witten theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 29 January 2018, pp. 595-620
- Print publication:
- March 2018
-
- Article
- Export citation
CANONICAL LIFTS OF FAMILIES OFELLIPTIC CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 02 November 2017, pp. 193-213
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation