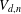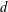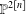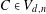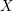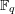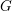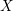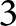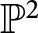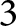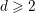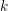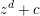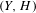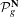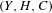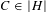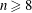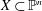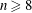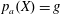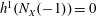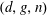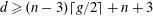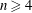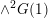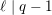Refine listing
Actions for selected content:
300 results in 14Hxx
ON THE POSITION OF NODES OF PLANE CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 01 June 2020, pp. 62-68
- Print publication:
- February 2021
-
- Article
- Export citation
Cuspidal cohomology of stacks of shtukas
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 14 May 2020, pp. 1079-1151
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Complete Classification of 3-dimensional Quadratic AS-regular Algebras of Type EC
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 123-141
- Print publication:
- March 2021
-
- Article
- Export citation
Principal co-Higgs bundles on ℙ1
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 05 March 2020, pp. 512-530
-
- Article
- Export citation
Gonality of dynatomic curves and strong uniform boundedness of preperiodic points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 17 February 2020, pp. 733-743
- Print publication:
- April 2020
-
- Article
- Export citation
Generalized Beilinson Elements and Generalized Soulé Characters
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 06 February 2020, pp. 542-571
- Print publication:
- April 2021
-
- Article
- Export citation
LARGE FIELDS IN DIFFERENTIAL GALOIS THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 1931-1946
- Print publication:
- November 2021
-
- Article
- Export citation
Two-graphs and the Embedded Topology of Smooth Quartics and its Bitangent Lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 24 January 2020, pp. 802-812
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Triviality Properties of Principal Bundles on Singular Curves. II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 24 January 2020, pp. 423-433
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Belyi’s theorem in characteristic two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 325-339
- Print publication:
- February 2020
-
- Article
- Export citation
On square-free values of large polynomials over the rational function field
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 247-263
- Print publication:
- March 2021
-
- Article
- Export citation
HALF NIKULIN SURFACES AND MODULI OF PRYM CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 29 November 2019, pp. 1547-1584
- Print publication:
- September 2021
-
- Article
- Export citation
(t, ℓ)-STABILITY AND COHERENT SYSTEMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 09 October 2019, pp. 661-672
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
A Vanishing Theorem for the Twisted Normal Bundle of Curves in
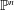 $\mathbb{P}^{n}$,
$\mathbb{P}^{n}$, 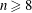 $n\geqslant 8$
$n\geqslant 8$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 30 August 2019, pp. 1-5
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
EXTENDING THE DOUBLE RAMIFICATION CYCLE BY RESOLVING THE ABEL-JACOBI MAP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 20 May 2019, pp. 331-359
- Print publication:
- January 2021
-
- Article
-
- You have access
- Open access
- Export citation
CONSTANCY OF NEWTON POLYGONS OF
 $F$-ISOCRYSTALS ON ABELIAN VARIETIES AND ISOTRIVIALITY OF FAMILIES OF CURVES
$F$-ISOCRYSTALS ON ABELIAN VARIETIES AND ISOTRIVIALITY OF FAMILIES OF CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 14 May 2019, pp. 587-625
- Print publication:
- March 2021
-
- Article
- Export citation
Primes Dividing Invariants of CM Picard Curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 480-504
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
The Action of a Plane Singular Holomorphic Flow on a Non-invariant Branch
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 22 April 2019, pp. 835-866
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Geometric Manin’s conjecture and rational curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 10 April 2019, pp. 833-862
- Print publication:
- May 2019
-
- Article
- Export citation
Cohen–Lenstra heuristics for étale group schemes and symplectic pairings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 758-775
- Print publication:
- April 2019
-
- Article
- Export citation