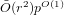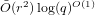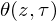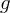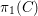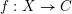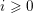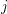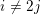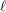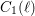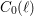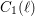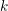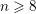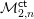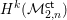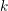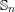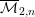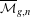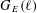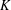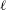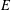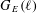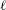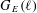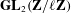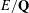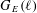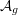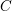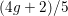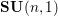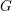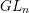Refine listing
Actions for selected content:
300 results in 14Hxx
Explicit isogenies in quadratic time in any characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 267-282
-
- Article
-
- You have access
- Export citation
A database of genus-2 curves over the rational numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 235-254
-
- Article
-
- You have access
- Export citation
JKL-ECM: an implementation of ECM using Hessian curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 83-99
-
- Article
-
- You have access
- Export citation
Computing theta functions in quasi-linear time in genus two and above
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 163-177
-
- Article
-
- You have access
- Export citation
Constructing genus-3 hyperelliptic Jacobians with CM
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 283-300
-
- Article
-
- You have access
- Export citation
Real multiplication through explicit correspondences
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 29-42
-
- Article
-
- You have access
- Export citation
Gonality of abstract modular curves in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 29 July 2016, pp. 2405-2442
- Print publication:
- November 2016
-
- Article
- Export citation
Tautological rings of spaces of pointed genus two curves of compact type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 17 June 2016, pp. 1398-1420
- Print publication:
- July 2016
-
- Article
- Export citation
MODULI SPACES OF RATIONAL WEIGHTED STABLE CURVES AND TROPICAL GEOMETRY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 03 June 2016, e9
-
- Article
-
- You have access
- Open access
- Export citation
THE MODULI SPACE OF TWISTED CANONICAL DIVISORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 05 April 2016, pp. 615-672
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
GENERALIZED EXPLICIT DESCENT AND ITS APPLICATION TO CURVES OF GENUS 3
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, e6
-
- Article
-
- You have access
- Open access
- Export citation
ALGORITHMS FOR GALOIS EXTENSIONS OF GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 513-515
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
COMPUTING IMAGES OF GALOIS REPRESENTATIONS ATTACHED TO ELLIPTIC CURVES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 02 February 2016, e4
-
- Article
-
- You have access
- Open access
- Export citation
On the Oort conjecture for Shimura varieties of unitary and orthogonal types
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 889-917
- Print publication:
- May 2016
-
- Article
- Export citation
Some non-finitely generated Cox rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 984-996
- Print publication:
- May 2016
-
- Article
- Export citation
Good families of Drinfeld modular curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 699-712
-
- Article
-
- You have access
- Export citation
CERTAIN GENERALIZED MORDELL CURVES OVER THE RATIONAL NUMBERS ARE POINTLESS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 28 October 2015, pp. 42-64
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
PARAMETRIZING ELLIPTIC CURVES BY MODULAR UNITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 19 August 2015, pp. 33-41
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Compactifications of reductive groups as moduli stacks of bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 18 August 2015, pp. 62-98
- Print publication:
- January 2016
-
- Article
- Export citation
The Hele-Shaw flow and moduli of holomorphic discs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 18 August 2015, pp. 2301-2328
- Print publication:
- December 2015
-
- Article
- Export citation