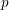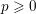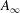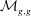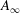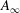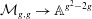Refine listing
Actions for selected content:
300 results in 14Hxx
ON THE NUMBER OF RATIONAL POINTS ON PRYM VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 55-68
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
Topological realizations and fundamental groups of higher-rank graphs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 143-168
-
- Article
- Export citation
Hilbert–Mumford criterion for nodal curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 10 June 2015, pp. 2076-2130
- Print publication:
- November 2015
-
- Article
- Export citation
FORMAL GROUPS AND INVARIANT DIFFERENTIALS OF ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 May 2015, pp. 44-51
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
THE DISTRIBUTION OF 2-SELMER RANKS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH PARTIAL TWO-TORSION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 04 May 2015, pp. 67-78
- Print publication:
- 2016
-
- Article
- Export citation
Elliptic Springer theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 08 April 2015, pp. 1568-1584
- Print publication:
- August 2015
-
- Article
- Export citation
Restrictions on the prime-to-
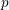 $p$ fundamental group of a smooth projective variety
$p$ fundamental group of a smooth projective variety
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 1083-1095
- Print publication:
- June 2015
-
- Article
- Export citation
GAPS IN TAYLOR SERIES OF ALGEBRAIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 412-418
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF ELLIPTIC CURVES WITH PRESCRIBED ISOGENY OR TORSION GROUP OVER NUMBER FIELDS OF PRIME DEGREE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 465-473
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
HEEGAARD FLOER HOMOLOGY AND RATIONAL CUSPIDAL CURVES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 05 December 2014, e28
-
- Article
-
- You have access
- Open access
- Export citation
A MINIMAL SET OF GENERATORS FOR THE CANONICAL IDEAL OF A NONDEGENERATE CURVE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 311-323
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
ON POSITIVE PROPORTION OF RANK-ZERO TWISTS OF ELLIPTIC CURVES OVER
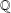 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 07 November 2014, pp. 281-288
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Computation on elliptic curves with complex multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 October 2014, pp. 509-535
-
- Article
-
- You have access
- Export citation
Numerical calculation of three-point branched covers of the projective line
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 379-430
-
- Article
-
- You have access
- Export citation
Minimal models for
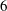 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}6$-coverings of elliptic curves
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}6$-coverings of elliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 112-127
-
- Article
-
- You have access
- Export citation
Parametrizing the moduli space of curves and applications to smooth plane quartics over finite fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 128-147
-
- Article
-
- You have access
- Export citation
Universal polynomials for singular curves on surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 06 June 2014, pp. 1169-1182
- Print publication:
- July 2014
-
- Article
- Export citation
ELLIPTIC CURVES ARISING FROM BRAHMAGUPTA QUADRILATERALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 47-56
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
On a conjecture of Rudin on squares in arithmetic progressions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 58-76
-
- Article
-
- You have access
- Export citation
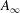 $A_{\infty }$-algebras associated with curves and rational functions on
$A_{\infty }$-algebras associated with curves and rational functions on 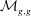 $\mathcal{M}_{g,g}$. I
$\mathcal{M}_{g,g}$. I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 621-667
- Print publication:
- April 2014
-
- Article
- Export citation