Refine listing
Actions for selected content:
300 results in 14Hxx
The non-existence of stable Schottky forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 679-690
- Print publication:
- April 2014
-
- Article
- Export citation
On the algebraic independence of generic Painlevé transcendents
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 668-678
- Print publication:
- April 2014
-
- Article
- Export citation
ON THE NILPOTENT SECTION CONJECTURE FOR FINITE GROUP ACTIONS ON CURVES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 13 December 2013, pp. 183-200
- Print publication:
- January 2014
-
- Article
- Export citation
Kummer covers and braid monodromy
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 17 October 2013, pp. 633-670
- Print publication:
- July 2014
-
- Article
- Export citation
Derived categories and rationality ofconic bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1789-1817
- Print publication:
- November 2013
-
- Article
- Export citation
A vanishing theorem and symbolic powers of planar point ideals
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 373-387
-
- Article
-
- You have access
- Export citation
PARABOLIC HIGGS BUNDLES AND
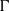 $\Gamma $-HIGGS BUNDLES
$\Gamma $-HIGGS BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 19 August 2013, pp. 315-328
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Brill–Noether loci in codimension two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 1535-1568
- Print publication:
- September 2013
-
- Article
- Export citation
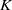 $K$ -theory of one-dimensional rings via pro-excision
$K$ -theory of one-dimensional rings via pro-excision
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 23 July 2013, pp. 225-272
- Print publication:
- April 2014
-
- Article
- Export citation
Complexity of OM factorizations of polynomials over local fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 June 2013, pp. 139-171
-
- Article
-
- You have access
- Export citation
Rationality of fields of invariants for some representations ofSL2 × SL2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 22 May 2013, pp. 1225-1234
- Print publication:
- July 2013
-
- Article
- Export citation
SOME INDEX FORMULAE ON THE MODULI SPACE OF STABLE PARABOLIC VECTOR BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 1-37
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 29 January 2013, pp. 705-728
- Print publication:
- April 2013
-
- Article
- Export citation
ON SELMER GROUPS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH A TWO-TORSION OVER
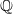 $\mathbb {Q}$
$\mathbb {Q}$
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 15 January 2013, pp. 303-319
- Print publication:
- July 2013
-
- Article
- Export citation
Identifying supersingular elliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 317-325
-
- Article
-
- You have access
- Export citation
Symplectic T7, T8 singularities and Lagrangian tangency orders
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 28 August 2012, pp. 657-683
-
- Article
-
- You have access
- Export citation
Accelerating the CM method
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 172-204
-
- Article
-
- You have access
- Export citation
Generic Torelli theorem for Prym varieties of ramified coverings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 11 July 2012, pp. 1147-1170
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
K1(
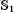 ) and the group of automorphisms of the algebra
) and the group of automorphisms of the algebra 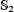 of one-sided inverses of a polynomial algebra in two variables
of one-sided inverses of a polynomial algebra in two variables
- Part of
-
- Journal:
- Journal of K-Theory / Volume 10 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 24 May 2012, pp. 583-601
- Print publication:
- December 2012
-
- Article
- Export citation
ON SELMER GROUPS AND TATE–SHAFAREVICH GROUPS FOR ELLIPTIC CURVES y2=x3−n3
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 236-274
- Print publication:
- July 2012
-
- Article
- Export citation
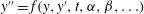
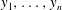
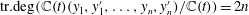
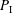
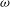
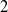
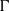
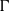
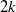
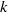
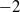
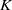
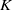
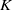
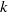

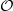
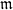
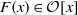

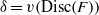
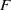
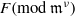

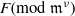
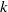
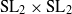
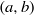
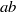
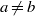

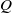
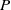
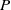
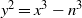
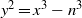
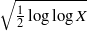
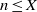
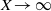

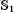 ) and the group of automorphisms of the algebra
) and the group of automorphisms of the algebra 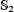 of one-sided inverses of a polynomial algebra in two variables
of one-sided inverses of a polynomial algebra in two variables
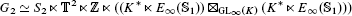
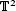 is the 2-dimensional algebraic torus,
is the 2-dimensional algebraic torus, 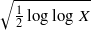 as
as 