We compare the cohomology of (parabolic) Hitchin fibers for Langlands dual groups G and G∨. The comparison theorem fits in the framework of the global Springer theory developed by the author. We prove that the stable parts of the parabolic Hitchin complexes for Langlands dual group are naturally isomorphic after passing to the associated graded of the perverse filtration. Moreover, this isomorphism intertwines the global Springer action on one hand and Chern class action on the other. Our result is inspired by the mirror symmetric viewpoint of geometric Langlands duality. Compared to the pioneer work in this subject by T. Hausel and M. Thaddeus, R. Donagi and T. Pantev, and N. Hitchin, our result is valid for more general singular fibers. The proof relies on a variant of Ngô’s support theorem, which is a key point in the proof of the Fundamental Lemma.

Let C be a locally planar curve. Its versal deformation admits a stratification by the genera of the fibres. The strata are singular; we show that their multiplicities at the central point are determined by the Euler numbers of the Hilbert schemes of points on C. These Euler numbers have made two prior appearances. First, in certain simple cases, they control the contribution of C to the Pandharipande–Thomas curve counting invariants of three-folds. In this context, our result identifies the strata multiplicities as the local contributions to the Gopakumar–Vafa BPS invariants. Second, when C is smooth away from a unique singular point, a conjecture of Oblomkov and the present author identifies the Euler numbers of the Hilbert schemes with the ‘U(∞)’ invariant of the link of the singularity. We make contact with combinatorial ideas of Jaeger, and suggest an approach to the conjecture.

We prove the conjectural relations between Mahler measures and L-values of elliptic curves of conductors 20 and 24. We also present new hypergeometric expressions for L-values of elliptic curves of conductors 27 and 36. Furthermore, we prove a new functional equation for the Mahler measure of the polynomial family (1+X) (1+Y )(X+Y )−αXY, α∈ℝ.

We develop the theory of Abelian functions associated with algebraic curves. The growth in computer power and the advancement of efficient symbolic computation techniques have allowed for recent progress in this area. In this paper we focus on the genus three cases, comparing the two canonical classes of hyperelliptic and trigonal curves. We present new addition formulae, derive bases for the spaces of Abelian functions and discuss the differential equations such functions satisfy.

Supplementary materials are available with this article.

We prove that the moduli spaces of n-pointed m-stable curves introduced in our previous paper have projective coarse moduli. We use the resulting spaces to run an analogue of Hassett’s log minimal model program for .

The set of non-constant holomorphic mappings between two given compact Riemann surfaces of genus greater than 1 is always finite. This classical statement was made by de Franchis. Furthermore, bounds on the cardinality of the set depending only on the genera of the surfaces have been obtained by a number of mathematicians. The analysis is carried over in this paper to the case of Riemann surfaces of finite analytic type (i.e. compact Riemann surfaces minus a finite set of points) so that the finiteness result, together with a crude but explicit bound depending only on the topological data, may be extended for the number of holomorphic mappings between such surfaces.

The moduli space of holomorphic maps from Riemann surfaces to the Grassmannian is known to have two kinds of compactifications: Kontsevich’s stable map compactification and Marian–Oprea–Pandharipande’s stable quotient compactification. Over a non-singular curve, the latter moduli space is Grothendieck’s Quot scheme. In this paper, we give the notion of ‘ ϵ-stable quotients’ for a positive real number ϵ, and show that stable maps and stable quotients are related by wall-crossing phenomena. We will also discuss Gromov–Witten type invariants associated to ϵ-stable quotients, and investigate them under wall crossing.

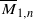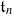Gaudin subalgebras are abelian Lie subalgebras of maximal dimension spanned by generators of the Kohno–Drinfeld Lie algebra . We show that Gaudin subalgebras form a variety isomorphic to the moduli space 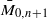of stable curves of genus zero with 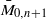n+1 marked points. In particular, this gives an embedding of in a Grassmannian of (n−1)-planes in an n(n−1)/2-dimensional space. We show that the sheaf of Gaudin subalgebras over is isomorphic to a sheaf of twisted first-order differential operators. For each representation of the Kohno–Drinfeld Lie algebra with fixed central character, we obtain a sheaf of commutative algebras whose spectrum is a coisotropic subscheme of a twisted version of the logarithmic cotangent bundle of .

Let C be a proper smooth geometrically connected hyperbolic curve over a field of characteristic 0 and ℓ a prime number. We prove the injectivity of the homomorphism from the pro-ℓ mapping class group attached to the two dimensional configuration space of C to the one attached to C, induced by the natural projection. We also prove a certain graded Lie algebra version of this injectivity. Consequently, we show that the kernel of the outer Galois representation on the pro-ℓ pure braid group on C with n strings does not depend on n, even if n = 1. This extends a previous result by Ihara–Kaneko. By applying these results to the universal family over the moduli space of curves, we solve completely Oda's problem on the independency of certain towers of (infinite) algebraic number fields, which has been studied by Ihara, Matsumoto, Nakamura, Ueno and the author. Sequentially we obtain certain information of the image of this Galois representation and get obstructions to the surjectivity of the Johnson–Morita homomorphism at each sufficiently large even degree (as Oda predicts), for the first time for a proper curve.

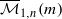We introduce a sequence of isolated curve singularities, the elliptic m-fold points, and an associated sequence of stability conditions, generalizing the usual definition of Deligne–Mumford stability. For every pair of integers 1≤m<n, we prove that the moduli problem of n-pointed m-stable curves of arithmetic genus one is representable by a proper irreducible Deligne–Mumford stack . We also consider weighted variants of these stability conditions, and construct the corresponding moduli stacks 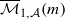. In forthcoming work, we will prove that these stacks have projective coarse moduli and use the resulting spaces to give a complete description of the log minimal model program for .

We discuss the Mordell–Weil sieve as a general technique for proving results concerning rational points on a given curve. In the special case of curves of genus 2, we describe quite explicitly how the relevant local information can be obtained if one does not want to restrict to mod p information at primes of good reduction. We describe our implementation of the Mordell–Weil sieve algorithm and discuss its efficiency.

Supplementary materials are available with this article.

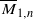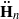We exhibit a strong link between the Hall algebra HX of an elliptic curve X defined over a finite field 𝔽l (or, more precisely, its spherical subalgebra U+X) and Cherednik’s double affine Hecke algebras of type GLn, for all n. This allows us to obtain a geometric construction of the Macdonald polynomials Pλ(q,t−1) in terms of certain functions (Eisenstein series) on the moduli space of semistable vector bundles on the elliptic curve X.

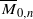We give a construction of the moduli space of stable maps to the classifying stack Bμr of a cyclic group by a sequence of rth root constructions on . We prove a closed formula for the total Chern class of μr-eigenspaces of the Hodge bundle, and thus of the obstruction bundle of the genus-zero Gromov–Witten theory of stacks of the form [ℂN/μr]. We deduce linear recursions for genus-zero Gromov–Witten invariants.

Let E/k be a function field over an infinite field of constants. Assume that E/k(x) is a separable extension of degree greater than one such that there exists a place of degree one of k(x) ramified in E. Let K/k be a function field. We prove that there exist infinitely many nonisomorphic separable extensions L/K such that [L:K]=[E:k(x)] and AutkL=AutKL≅Autk(x)E.

We realize the multiplihedron geometrically as the moduli space of stable quilted disks. This generalizes the geometric realization of the associahedron as the moduli space of stable disks. We show that this moduli space is the non-negative real part of a complex moduli space of stable scaled marked curves.

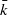Let k be a field of characteristic other than 2. There can be an obstruction to a principally polarized abelian threefold (A,a) over k, which is a Jacobian over , being a Jacobian over k; this can be computed in terms of the rationality of the square root of the value of a certain Siegel modular form. We show how to do this explicitly for principally polarized abelian threefolds which are the third power of an elliptic curve with complex multiplication. We use our numerical results to prove or refute the existence of some optimal curves of genus 3.

We study the automorphism groups of the reduction of a modular curve X0(N) over primes p∤N.

A foliation on a non-singular projective variety is algebraically integrable if all leaves are algebraic subvarieties. A non-singular hypersurface X in a non-singular projective variety M equipped with a symplectic form has a naturally defined foliation, called the characteristic foliation on X. We show that if X is of general type and dim M≥4, then the characteristic foliation on X cannot be algebraically integrable. This is a consequence of a more general result on Iitaka dimensions of certain invertible sheaves associated with algebraically integrable foliations by curves. The latter is proved using the positivity of direct image sheaves associated to families of curves.

We introduce in this paper a hypercohomology version of the resonance varieties and obtain some relations to the characteristic varieties of rank one local systems on a smooth quasi-projective complex variety M. A logarithmic resonance variety is also considered and, as an application, we determine the first characteristic variety of the configuration space of n distinct labeled points on an elliptic curve. Finally, for a logarithmic 1-form α on M we investigate the relation between the resonance degree of α and the codimension of the zero set of α on a good compactification of M. This question was inspired by the recent work by Cohen, Denham, Falk and Varchenko.

If C is a curve of genus 2 defined over a field k and J is its Jacobian, then we can associate a hypersurface K in ℙ3 to J, called the Kummer surface of J. Flynn has made this construction explicit in the case when the characteristic of k is not 2 and C is given by a simplified equation. He has also given explicit versions of several maps defined on the Kummer surface and shown how to perform arithmetic on J using these maps. In this paper we generalize these results to the case of arbitrary characteristic.