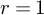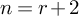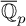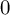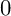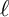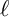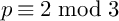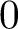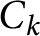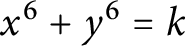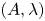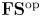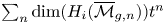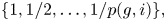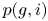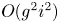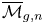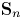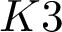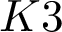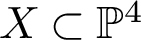Refine listing
Actions for selected content:
300 results in 14Hxx
The symplectic isotopy problem for rational cuspidal curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 16 September 2022, pp. 1595-1682
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vector bundles and finite covers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR SERIES ON GENERAL CURVES WITH PRESCRIBED INCIDENCE CONDITIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2857-2877
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE TEMPERED FUNDAMENTAL GROUPS OF HYPERBOLIC CURVES OF GENUS
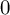 $0$ OVER
$0$ OVER 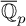 $\overline {\mathbb {Q}}_p$
$\overline {\mathbb {Q}}_p$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 01 June 2022, pp. 2833-2856
- Print publication:
- November 2023
-
- Article
- Export citation
THE BOUNDARY OF THE p-RANK
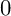 $0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 865-887
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chow rings of stacks of prestable curves I
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 26 May 2022, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE LOCAL-ORBIFOLD CORRESPONDENCE FOR SIMPLE NORMAL CROSSING PAIRS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 2515-2531
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integers that are sums of two rational sixth powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 166-177
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kirchhoff’s theorem for Prym varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 February 2022, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gromov–Witten theory with maximal contacts
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 24 January 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Faltings height and Néron–Tate height of a theta divisor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 1-32
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tevelev degrees and Hurwitz moduli spaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 03 December 2021, pp. 479-510
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability in the homology of Deligne–Mumford compactifications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 17 December 2021, pp. 2635-2656
- Print publication:
- December 2021
-
- Article
- Export citation
CONICS IN SEXTIC
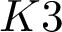 $K3$-SURFACES IN
$K3$-SURFACES IN  $\mathbb {P}^4$
$\mathbb {P}^4$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 29 November 2021, pp. 273-304
- Print publication:
- June 2022
-
- Article
- Export citation
ON THE CHOW THEORY OF PROJECTIVIZATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 11 November 2021, pp. 1465-1508
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological invariants of root stacks and admissible double coverings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 November 2021, pp. 202-224
- Print publication:
- February 2023
-
- Article
- Export citation
Free quotients of fundamental groups of smooth quasi-projective varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 27 October 2021, pp. 924-946
-
- Article
- Export citation
Non-uniform ergodic properties of Hamiltonian flows with impacts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 20 October 2021, pp. 190-252
- Print publication:
- January 2023
-
- Article
- Export citation
Brauer groups of moduli of hyperelliptic curves via cohomological invariants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 17 September 2021, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinitesimal structure of the pluricanonical double ramification locus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2280-2337
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation