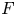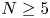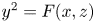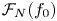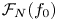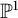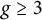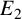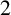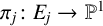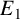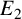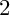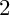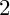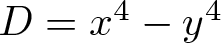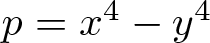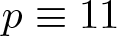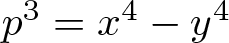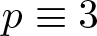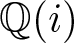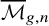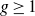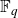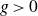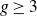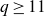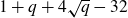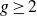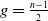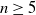Refine listing
Actions for selected content:
300 results in 14Hxx
Most odd-degree binary forms fail to primitively represent a square
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 481-517
- Print publication:
- March 2024
-
- Article
- Export citation
TOPICS SURROUNDING THE COMBINATORIAL ANABELIAN GEOMETRY OF HYPERBOLIC CURVES IV: DISCRETENESS AND SECTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 18 January 2024, pp. 785-885
- Print publication:
- December 2024
-
- Article
- Export citation
Relations for quadratic Hodge integrals via stable maps
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 680-686
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Refinements of Katz–Sarnak theory for the number of points on curves over finite fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 09 January 2024, pp. 400-425
- Print publication:
- April 2025
-
- Article
- Export citation
INTERSECTING THE TORSION OF ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 56-63
- Print publication:
- August 2024
-
- Article
- Export citation
THE CERESA CLASS: TROPICAL, TOPOLOGICAL AND ALGEBRAIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 21 December 2023, pp. 2175-2215
- Print publication:
- September 2024
-
- Article
- Export citation
LOCAL SECTIONS OF ARITHMETIC FUNDAMENTAL GROUPS OF p-ADIC CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 20 December 2023, pp. 462-487
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENUS
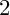 $2$ CURVES WITH BAD REDUCTION AT ONE ODD PRIME
$2$ CURVES WITH BAD REDUCTION AT ONE ODD PRIME
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 498-512
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the difference of two fourth powers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 142-150
-
- Article
- Export citation
Notes on hyperelliptic mapping class groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 126-161
- Print publication:
- January 2024
-
- Article
- Export citation
Interpolation for Brill–Noether curves
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 October 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian tropical covers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 October 2023, pp. 395-416
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonvarying, affine and extremal geometry of strata of differentials
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 361-371
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth Compactifications of the Abel-Jacobi Section
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 October 2023, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower bounds on the maximal number of rational points on curves over finite fields
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 213-238
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A BALL QUOTIENT PARAMETRIZING TRIGONAL GENUS 4 CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 21 September 2023, pp. 366-378
- Print publication:
- June 2024
-
- Article
- Export citation
Derived Category and ACM Bundles of Moduli Space of Vector Bundles on a Curve
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 September 2023, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 29 August 2023, pp. 2191-2259
- Print publication:
- October 2023
-
- Article
- Export citation
Geometric aspects on Humbert-Edge curves of type 5, Kummer surfaces and hyperelliptic curves of genus 2
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 612-624
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Floor diagrams and enumerative invariants of line bundles over an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 07 July 2023, pp. 1741-1790
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation