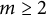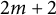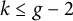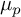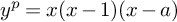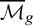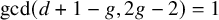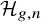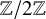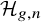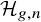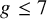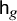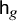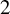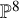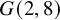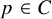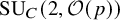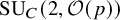Refine listing
Actions for selected content:
311 results in 14Hxx
Quasidiagonals in strata of translation surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 2233-2248
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the properness of the moduli space of stable surfaces over
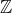 $\mathbb{Z}$[1/30]
$\mathbb{Z}$[1/30]
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Genus-zero r-spin theory
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The integral Chow ring of
 $\mathcal {M}_{1,n}$ for
$\mathcal {M}_{1,n}$ for  $n=3,\dots ,10$
$n=3,\dots ,10$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poncelet’s closure theorem and the embedded topology of conic-line arrangements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 109-123
- Print publication:
- March 2025
-
- Article
- Export citation
The line bundles on the moduli stack of principal bundles on families of curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 80-127
-
- Article
- Export citation
Non-torsion algebraic cycles on the Jacobians of Fermat quotients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 60-72
- Print publication:
- March 2025
-
- Article
- Export citation
ARBITRARILY LARGE p-TORSION IN TATE-SHAFAREVICH GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 481-502
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ODA’S PROBLEM AND SPECIAL LOCI
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 503-539
- Print publication:
- March 2025
-
- Article
- Export citation
Period realization of meromorphic differentials with prescribed invariants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 November 2024, e90
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability conditions for line bundles on nodal curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THEOREM OF WARD ON SYMMETRIES OF ELLIPTIC NETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 93-106
- Print publication:
- February 2025
-
- Article
- Export citation
Tropical curves in abelian surfaces I: enumeration of curves passing through points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 109-148
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Failure of Galois Descent for p-Selmer Groups of Elliptic Curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 185-218
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sums of squares, Hankel index and almost real rank
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the weight zero compactly supported cohomology of
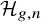 ${\mathcal {H}}_{g,n}$
${\mathcal {H}}_{g,n}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Globally F-regular type of the moduli spaces of parabolic symplectic/orthogonal bundles on curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic coverings of genus
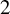 $2$ curves of Sophie Germain type
$2$ curves of Sophie Germain type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 May 2024, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Coble quadric
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 May 2024, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral decomposition of genuine cusp forms over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1194-1260
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation