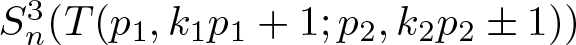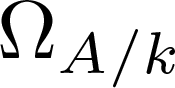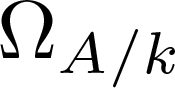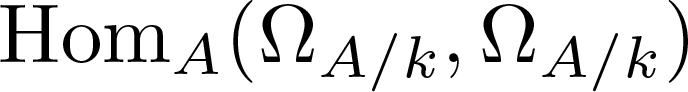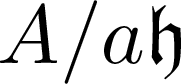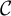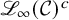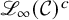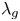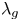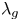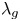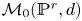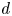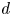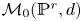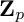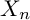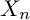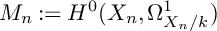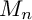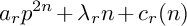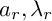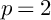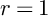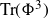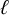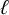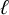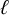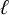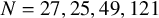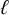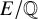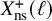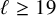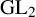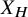Refine listing
Actions for selected content:
300 results in 14Hxx
On the algebra of elliptic curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 548-556
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surgeries on iterated torus knots bounding rational homology 4-balls
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 June 2023, pp. 557-578
-
- Article
- Export citation
Nonemptiness of severi varieties on enriques surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 June 2023, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On one-dimensional local rings and Berger’s conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 May 2023, pp. 437-452
-
- Article
- Export citation
Integral Fourier transforms and the integral Hodge conjecture for one-cycles on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1188-1213
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 301-315
- Print publication:
- April 2024
-
- Article
- Export citation
Arakelov–Milnor inequalities and maximal variations of Hodge structure
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 1005-1041
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of arcs and comparison of formal neighborhoods for a curve singularity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 April 2023, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wonderful compactifications and rational curves with cyclic action
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 April 2023, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unipotent nearby cycles and the cohomology of shtukas
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 590-615
- Print publication:
- March 2023
-
- Article
- Export citation
On some hyperelliptic Hurwitz–Hodge integrals
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 271-284
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hodge bundle, the universal 0-section, and the log Chow ring of the moduli space of curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 306-354
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The integral Chow ring of
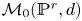 $\mathcal {M}_{0}(\mathbb {P}^r, d)$, for
$\mathcal {M}_{0}(\mathbb {P}^r, d)$, for 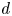 $d$ odd
$d$ odd
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 184-206
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic dynamics of the pentagram map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 3460-3505
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FROBENIUS-AFFINE STRUCTURES AND TANGO CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 385-409
- Print publication:
- June 2023
-
- Article
- Export citation
IWASAWA THEORY FOR p-TORSION CLASS GROUP SCHEMES IN CHARACTERISTIC p
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 298-351
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An algebraic approach to a quartic analogue of the Kontsevich model
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 471-495
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
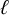 $\ell $-adic images of Galois for elliptic curves over
$\ell $-adic images of Galois for elliptic curves over  $\mathbb {Q}$ (and an appendix with John Voight)
$\mathbb {Q}$ (and an appendix with John Voight)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 August 2022, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A GENERALISATION OF WITTEN’S CONJECTURE FOR THE PIXTON CLASS AND THE NONCOMMUTATIVE KDV HIERARCHY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 18 July 2022, pp. 2987-3009
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The logarithmic Picard group and its tropicalization
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 09 September 2022, pp. 1477-1562
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation