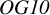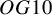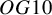Refine listing
Actions for selected content:
371 results in 14Jxx
Equivariant Segre and Verlinde invariants for Quot schemes
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXCEPTIONAL PAIRS ON DEL PEZZO SURFACES AND SPACES OF COMPATIBLE FEIGIN-ODESSKII BRACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-35
-
- Article
- Export citation
The KSBA moduli space of stable log Calabi–Yau surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable degeneration of families of klt singularities with constant local volume
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 29 September 2025, e158
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foldable fans, cscK surfaces and local K-moduli
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BLOWN-UP BOUNDARIES ASSOCIATED WITH AMPLE CONES OF K3 SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 23 September 2025, pp. 1-30
-
- Article
- Export citation
EFFECTIVE BOUND FOR SINGULARITIES ON TORIC FIBRATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1-17
-
- Article
-
- You have access
- HTML
- Export citation
K3 SURFACES AND ORTHOGONAL MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-41
-
- Article
- Export citation
On K-stability of blow-ups of weighted projective planes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-17
-
- Article
- Export citation
Minimal Kinematics on
 $\mathcal{M}_{0,n}$
$\mathcal{M}_{0,n}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mirror symmetry for log Calabi–Yau surfaces II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 22 October 2025, pp. 2025-2090
- Print publication:
- August 2025
-
- Article
- Export citation
Lagrangian families of Bridgeland moduli spaces from Gushel–Mukai fourfolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 09 October 2025, pp. 2091-2135
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant Fukaya categories at singular values
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite groups of symplectic birational transformations of IHS manifolds of
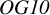 $\mathit {OG10}$ type
$\mathit {OG10}$ type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e117
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moments, Exponential Sums, and Monodromy Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smoothing surfaces on fourfolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MIRROR SYMMETRY FOR TROPICAL HYPERSURFACES AND PATCHWORKING
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 June 2025, pp. 2387-2425
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic singularities and threefold flops in positive characteristic
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1188-1244
-
- Article
- Export citation
Inversion of Adjunction for the minimal exponent
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic Chow stability of symmetric reflexive toric varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation