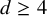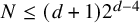Refine listing
Actions for selected content:
199 results in 14Mxx
Degeneracy locus formulas for amenable Weyl group elements
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 22 January 2026, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMAL SPLIT DIVISORS IN RATIONAL HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 12 January 2026, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Čech cohomology of infinite projective spaces, flag manifolds, and related spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 23 December 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the rationality problem for low degree hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 December 2025, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Toric arc schemes and q-enumeration of lattice points
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 December 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel-type presentation of the torus-equivariant quantum K-ring of flag manifolds of type C
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 December 2025, e198
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free fermionic probability theory and k-theoretic schubert calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 09 December 2025, e197
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Root, flow and order polytopes with connections to toric geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 November 2025, e194
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Initial degenerations of flag varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 10 November 2025, pp. 403-431
- Print publication:
- March 2026
-
- Article
- Export citation
The geometric Satake equivalence for integral motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 17 December 2025, pp. 2755-2851
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some algebraic properties of ASM varieties
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 October 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vanishing of Schubert coefficients via the effective Hilbert nullstellensatz
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 October 2025, e162
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foldable fans, cscK surfaces and local K-moduli
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EFFECTIVE BOUND FOR SINGULARITIES ON TORIC FIBRATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 779-795
-
- Article
-
- You have access
- HTML
- Export citation
Quantum K theory of Grassmannians, Wilson line operators and Schur bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 September 2025, e140
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cycles relations in the affine Grassmannian and applications to the Breuil–Mézard conjecture for G-crystalline representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 03 November 2025, pp. 2320-2372
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regularity and multiplicity of Veronese type algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 69 / Issue 1 / March 2026
- Published online by Cambridge University Press:
- 08 August 2025, pp. 150-178
- Print publication:
- March 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the formal Peterson subalgebra and its dual
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TORSION BIRATIONAL MOTIVES OF SURFACES AND UNRAMIFIED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 2283-2315
- Print publication:
- November 2025
-
- Article
-
- You have access
- HTML
- Export citation
Smooth locus of twisted affine Schubert varieties and twisted affine Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation