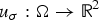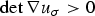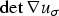Refine listing
Actions for selected content:
41 results in 49Nxx
A probabilistic verification theorem for the finite horizon two-player zero-sum optimal switching game in continuous time
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 425-442
- Print publication:
- June 2019
-
- Article
- Export citation
On c-cyclical monotonicity for optimal transport problem with Coulomb cost
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 23 May 2019, pp. 1210-1219
-
- Article
- Export citation
Twists and shear maps in nonlinear elasticity: explicit solutions and vanishing Jacobians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 41-71
- Print publication:
- February 2020
-
- Article
- Export citation
On the boundary regularity of phase-fields for Willmore's energy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1017-1035
- Print publication:
- August 2019
-
- Article
- Export citation
A new class of costs for optimal transport planning
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1229-1263
-
- Article
-
- You have access
- Export citation
Nash equilibria for nonzero-sum ergodic stochastic differential games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 977-994
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Impulse control and expected suprema
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 238-257
- Print publication:
- March 2017
-
- Article
- Export citation
The Variational Iteration Method for an Inverse Problem of Finding a Source Parameter
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 861-867
- Print publication:
- August 2017
-
- Article
- Export citation
METRIC REGULARITY—A SURVEY PART 1. THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 188-243
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
SUM THEOREMS FOR MAXIMALLY MONOTONE OPERATORS OF TYPE (FPV)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 1-26
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
FINSLER METRIZABLE ISOTROPIC SPRAYS AND HILBERT’S FOURTH PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 20 May 2014, pp. 27-47
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Bounded Variation Control of Itô Diffusions with Exogenously Restricted Intervention Times
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 102-120
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Convex Duality in Mean-Variance Hedging Under Convex Trading Constraints
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1084-1112
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Large deviations for a feed-forward network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 545-571
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
A TIME-FUEL OPTIMAL CONTROL PROBLEM OF A CRUISE MISSILE BASED ON AN IMPROVED SLIDING MODE VARIABLE STRUCTURE MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 02 June 2010, pp. 261-276
-
- Article
-
- You have access
- Export citation
A CLASS OF MIX DESIGN PROBLEMS: FORMULATION, SOLUTION METHODS AND APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 29 July 2009, pp. 455-474
-
- Article
-
- You have access
- Export citation
Maximization of the long-term growth rate for a portfolio with fixed and proportional transaction costs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 673-695
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Convex duality in constrained mean-variance portfolio optimization
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 77-104
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Optimal portfolio policies under fixed and proportional transaction costs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 08 September 2016, pp. 916-942
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
A note on long-term optimal portfolios under drawdown constraints
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 673-692
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation