Refine listing
Actions for selected content:
125 results in 13Axx
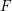 $F$ -PURITY VERSUS LOG CANONICITY FOR POLYNOMIALS
$F$ -PURITY VERSUS LOG CANONICITY FOR POLYNOMIALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 23 August 2016, pp. 10-36
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
THE
 ${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 08 July 2016, e5
-
- Article
-
- You have access
- Open access
- Export citation
Symbolic Powers of Monomial Ideals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 39-55
-
- Article
- Export citation
BERNSTEIN–SATO POLYNOMIALS AND TEST MODULES IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 74-99
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
Irreducible decomposition of binomial ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1319-1332
- Print publication:
- June 2016
-
- Article
- Export citation
Homaloidal nets and ideals of fat points I
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 54-77
-
- Article
-
- You have access
- Export citation
Upper semi-continuity of the Hilbert–Kunz multiplicity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 477-488
- Print publication:
- March 2016
-
- Article
- Export citation
TEST IDEALS IN RINGS WITH FINITELY GENERATED ANTI-CANONICAL ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 13 January 2016, pp. 171-206
- Print publication:
- February 2018
-
- Article
- Export citation
Zero-Separating Invariants for Linear Algebraic Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 911-924
-
- Article
- Export citation
The two-color Soergel calculus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 22 September 2015, pp. 327-398
- Print publication:
- February 2016
-
- Article
- Export citation
STABILITY PATTERNS IN REPRESENTATION THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 15 June 2015, e11
-
- Article
-
- You have access
- Open access
- Export citation
THE CATENARY DEGREE OF KRULL MONOIDS II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 324-354
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Parametrizing the moduli space of curves and applications to smooth plane quartics over finite fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 128-147
-
- Article
-
- You have access
- Export citation
The
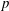 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 1125-1168
- Print publication:
- July 2014
-
- Article
- Export citation
On the family of affine threefolds
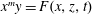 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 09 June 2014, pp. 979-998
- Print publication:
- June 2014
-
- Article
- Export citation
CAYLEY SUM GRAPHS OF IDEALS OF A COMMUTATIVE RING
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 16 June 2014, pp. 289-302
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
A vanishing theorem and symbolic powers of planar point ideals
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 373-387
-
- Article
-
- You have access
- Export citation
On the
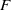 $F$-purity of isolated log canonical singularities
$F$-purity of isolated log canonical singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 20 June 2013, pp. 1495-1510
- Print publication:
- September 2013
-
- Article
- Export citation
Depth of
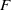 $F$-singularities and base change of relative canonical sheaves
$F$-singularities and base change of relative canonical sheaves
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 05 March 2013, pp. 43-63
- Print publication:
- January 2014
-
- Article
- Export citation
Complexity for modules over the classical Lie superalgebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1561-1592
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
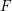
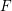
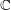
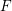
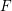
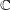
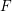

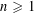
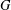
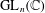
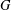
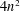
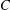
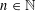
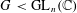
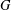
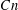

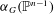
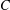
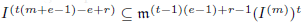 for all positive integers
for all positive integers 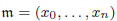 . This captures two conjectures (
. This captures two conjectures (
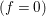
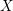
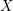
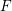

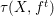
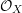
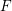
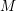
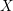
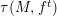
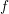
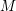

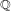
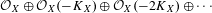


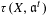
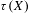

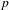
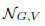 its null-cone. Let δ(
its null-cone. Let δ(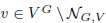 and
and 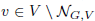 , respectively, there exists a homogeneous invariant
, respectively, there exists a homogeneous invariant 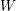
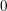
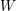

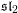
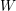
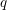
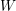
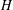
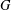
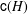
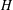
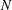
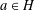
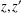

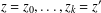

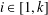
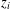
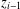
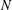
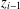
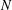
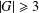
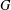
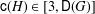
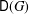
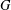
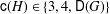
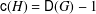
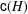
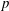
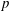
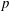
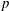
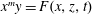
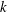
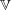
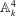
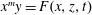
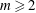
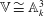
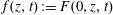
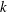
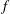
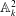
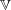
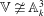
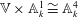
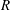
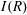
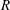
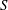
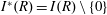
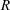
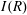
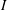
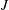
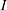
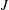

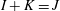
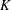
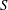
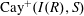
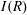
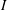
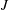
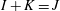
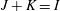
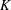
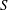
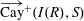
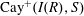
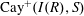
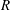
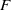
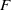
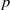
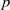
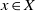
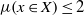
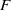
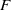
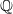
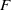
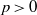
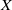
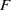
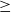
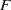
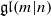
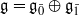 be a classical Lie superalgebra and let ℱ be the category of finite-dimensional
be a classical Lie superalgebra and let ℱ be the category of finite-dimensional 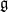 -supermodules which are completely reducible over the reductive Lie algebra
-supermodules which are completely reducible over the reductive Lie algebra 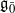 . In [B. D. Boe, J. R. Kujawa and D. K. Nakano,
. In [B. D. Boe, J. R. Kujawa and D. K. Nakano, 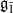 . In this paper we compute the complexity of the simple modules and the Kac modules for the Lie superalgebra
. In this paper we compute the complexity of the simple modules and the Kac modules for the Lie superalgebra 