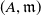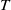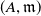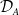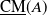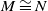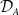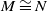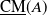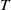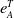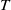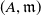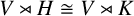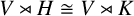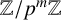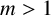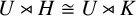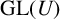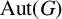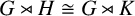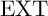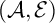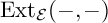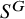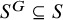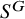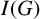Refine listing
Actions for selected content:
77 results in 13Cxx
Intersection Theorem for DG-modules over non-positive DG-rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-18
-
- Article
- Export citation
Silting, cosilting and extensions of commutative rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ideals and their Fitting ideals
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 30 July 2025, pp. 609-621
- Print publication:
- November 2025
-
- Article
- Export citation
Locally compact modules over abelian groups and compactly generated metabelian groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1250-1283
- Print publication:
- June 2025
-
- Article
- Export citation
Free summands of stably free modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 May 2025, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TENSOR PRODUCTS OF d-FOLD MATRIX FACTORIZATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 24 February 2025, e2
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOCAL COHOMOLOGY UNDER SMALL PERTURBATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 183-200
- Print publication:
- June 2025
-
- Article
- Export citation
Equivalences of stable categories of Gorenstein local rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 338-348
- Print publication:
- March 2025
-
- Article
- Export citation
A sub-functor for Ext and Cohen–Macaulay associated graded modules with bounded multiplicity-II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 30 October 2024, pp. 86-106
- Print publication:
- January 2025
-
- Article
- Export citation
Classification of multiplication modules over multiplication rings with finitely many minimal primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 67-71
- Print publication:
- January 2025
-
- Article
- Export citation
ISOMORPHISM OF RELATIVE HOLOMORPHS AND MATRIX SIMILARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 23 September 2024, pp. 298-313
- Print publication:
- April 2025
-
- Article
- Export citation
Annihilators and decompositions of singularity categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 23 April 2024, pp. 699-713
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lim Ulrich sequences and Boij-Söderberg cones
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e115
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOW TO EXTEND CLOSURE AND INTERIOR OPERATIONS TO MORE MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 513-560
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the reducing projective dimension over local rings
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 104-118
- Print publication:
- January 2024
-
- Article
- Export citation
EXACT SUBCATEGORIES, SUBFUNCTORS OF
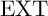 ${\operatorname{EXT}}$, AND SOME APPLICATIONS
${\operatorname{EXT}}$, AND SOME APPLICATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 379-419
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ulrich modules and weakly lim Ulrich sequences do not always exist
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 August 2023, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
When are the natural embeddings of classical invariant rings pure?
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projective freeness and stable rank of algebras of complex-valued BV functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 844-853
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REGULARITY OF POWERS OF BIPARTITE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1-9
- Print publication:
- February 2023
-
- Article
- Export citation