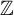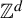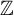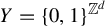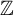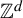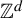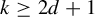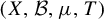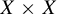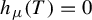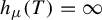Refine listing
Actions for selected content:
310 results in 37Bxx
Some hyperbolicity revisited and robust transitivity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 3800-3831
- Print publication:
- December 2025
-
- Article
- Export citation
Topological structure of isolated points in the space of
 $\mathbb {Z}^d$-shifts
$\mathbb {Z}^d$-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 3344-3376
- Print publication:
- November 2025
-
- Article
- Export citation
Hereditarily frequently hypercyclic operators and disjoint frequent hypercyclicity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 3021-3072
- Print publication:
- October 2025
-
- Article
- Export citation
Borel complexity of sets of points with prescribed Birkhoff averages in Polish dynamical systems with a specification property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 2695-2723
- Print publication:
- September 2025
-
- Article
- Export citation
On the algorithmic descriptive complexity of attractors in topological dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2533-2560
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transitive mappings on the Cantor fan
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2601-2635
- Print publication:
- September 2025
-
- Article
- Export citation
On partial rigidity of
 $\mathcal {S}$-adic subshifts
$\mathcal {S}$-adic subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2724-2764
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint transitivity for linear iterates
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 February 2025, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bender–Knuth Billiards in Coxeter Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A variational principle of scaled entropy for amenable group actions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-28
-
- Article
- Export citation
Buried points of plane continua
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 451-460
- Print publication:
- June 2025
-
- Article
- Export citation
Bounds for equilibrium states on amenable group subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 2414-2438
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An embedding theorem for multidimensional subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 1870-1914
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some remarks about self-products and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 2183-2193
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear repetitivity beyond abelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1947-1997
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lyapunov stability of non-isolated equilibria for strongly irreversible Allen–Cahn equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-21
-
- Article
- Export citation
Scaling limit of soliton lengths in a multicolor box-ball system
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shadowing and hyperbolicity for linear delay difference equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-30
-
- Article
- Export citation
Persistent properties from the Gromov–Hausdorff viewpoint
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1229-1240
-
- Article
- Export citation
A criterion to detect a non-trivial homology of an invariant set of a flow in
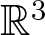 $\mathbb{R}^3$
$\mathbb{R}^3$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation