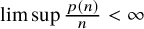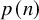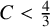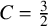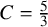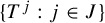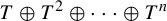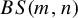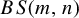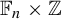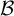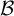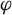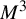Refine listing
Actions for selected content:
310 results in 37Bxx
Geometrical representation of subshifts for primitive substitutions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1885-1912
- Print publication:
- July 2024
-
- Article
- Export citation
Distortion element in the automorphism group of a full shift
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1757-1817
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Low complexity subshifts have discrete spectrum
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 October 2023, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Piecewise contracting maps on the interval: Hausdorff dimension, entropy, and attractors
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 21 September 2023, pp. 318-327
- Print publication:
- June 2024
-
- Article
- Export citation
Stability for hyperbolic groups acting on boundary spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 September 2023, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measure-theoretic sequence entropy pairs and mean sensitivity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 1531-1540
- Print publication:
- June 2024
-
- Article
- Export citation
Shape index, Brouwer degree and Poincaré–Hopf theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 September 2023, pp. 413-428
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WEAK HEIRS, COHEIRS, AND THE ELLIS SEMIGROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 166-187
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonchaotic N-expansive homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 31 August 2023, pp. 1-9
- Print publication:
- February 2025
-
- Article
- Export citation
Disjoint hypercyclicity, Sidon sets and weakly mixing operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1315-1329
- Print publication:
- May 2024
-
- Article
- Export citation
Tame or wild Toeplitz shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 1379-1417
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Encoding subshifts through sliding block codes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1609-1628
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orbits closeness for slowly mixing dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1192-1208
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuum of allosteric actions for non-amenable surface groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1581-1596
- Print publication:
- June 2024
-
- Article
- Export citation
On the abundance of k-fold semi-monotone minimal sets in bimodal circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 12 July 2023, pp. 1269-1314
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Word complexity of (measure-theoretically) weakly mixing rank-one subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 1330-1366
- Print publication:
- May 2024
-
- Article
- Export citation
Strongly aperiodic SFTs on generalized Baumslag–Solitar groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1209-1238
- Print publication:
- May 2024
-
- Article
- Export citation
Automorphisms of
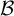 ${\mathcal B}$-free and other Toeplitz shifts
${\mathcal B}$-free and other Toeplitz shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1058-1101
- Print publication:
- April 2024
-
- Article
- Export citation
A word of low complexity without uniform frequencies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1013-1025
- Print publication:
- April 2024
-
- Article
- Export citation
Cancellations of periodic orbits for non-singular Morse–Smale flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 25 May 2023, pp. 1123-1171
- Print publication:
- April 2024
-
- Article
- Export citation