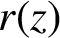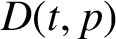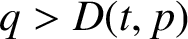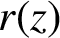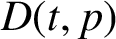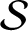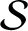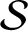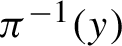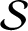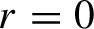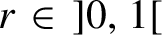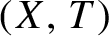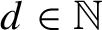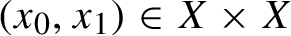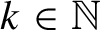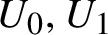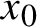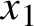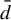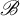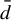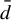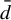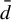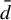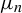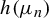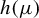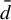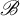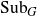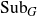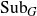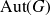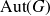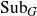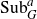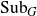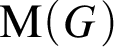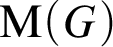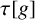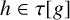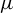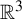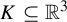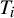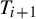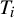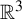Refine listing
Actions for selected content:
309 results in 37Bxx
SUBSHIFTS OF FINITE TYPE WITH A HOLE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 March 2022, pp. 73-98
- Print publication:
- August 2023
-
- Article
- Export citation
Symbolic factors of
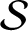 ${\mathcal S}$-adic subshifts of finite alphabet rank
${\mathcal S}$-adic subshifts of finite alphabet rank
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 17 March 2022, pp. 1511-1547
- Print publication:
- May 2023
-
- Article
- Export citation
FORCING CONSTRUCTIONS AND COUNTABLE BOREL EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 873-893
- Print publication:
- September 2022
-
- Article
- Export citation
Sur le spectre des opérateurs rigides
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 01 March 2022, pp. 1351-1362
- Print publication:
- April 2023
-
- Article
- Export citation
Covering action on Conley index theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 21 February 2022, pp. 1633-1665
- Print publication:
- May 2023
-
- Article
- Export citation
Independence and almost automorphy of higher order
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1363-1381
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
On
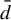 ${\bar d}$-approachability, entropy density and
${\bar d}$-approachability, entropy density and 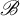 $\mathscr {B}$-free shifts
$\mathscr {B}$-free shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 943-970
- Print publication:
- March 2023
-
- Article
- Export citation
New approach to weighted topological entropy and pressure
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 28 January 2022, pp. 1004-1034
- Print publication:
- March 2023
-
- Article
- Export citation
Distal Actions of Automorphisms of Lie Groups G on SubG
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 21 December 2021, pp. 457-478
- Print publication:
- September 2022
-
- Article
- Export citation
Dendrites and measures with discrete spectrum
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 December 2021, pp. 545-555
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large deviation principle for piecewise monotonic maps with density of periodic measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 14 December 2021, pp. 861-872
- Print publication:
- March 2023
-
- Article
- Export citation
Entropy, products, and bounded orbit equivalence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 06 December 2021, pp. 904-942
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some Progress on the Unique Ergodicity Problem
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 February 2022, pp. 527-528
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
ORIENTATION OF PIECEWISE POWERS OF A MINIMAL HOMEOMORPHISM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 15 November 2021, pp. 226-256
- Print publication:
- October 2022
-
- Article
- Export citation
The type semigroup, comparison, and almost finiteness for ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 27 October 2021, pp. 361-400
- Print publication:
- February 2023
-
- Article
- Export citation
Generic properties of homeomorphisms preserving a given dynamical simplex
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 25 October 2021, pp. 646-662
- Print publication:
- February 2023
-
- Article
- Export citation
Packing topological entropy for amenable group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 20 October 2021, pp. 480-514
- Print publication:
- February 2023
-
- Article
- Export citation
The geometric index and attractors of homeomorphisms of
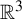 $\mathbb {R}^3$
$\mathbb {R}^3$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 50-77
- Print publication:
- January 2023
-
- Article
- Export citation
Homotopy Hubbard trees for post-singularly finite exponential maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 01 October 2021, pp. 253-298
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Loosely Bernoulli odometer-based systems whose corresponding circular systems are not loosely Bernoulli
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 917-973
- Print publication:
- March 2022
-
- Article
- Export citation