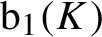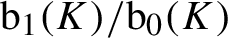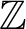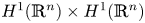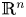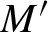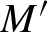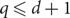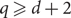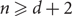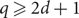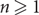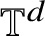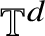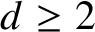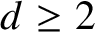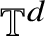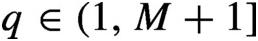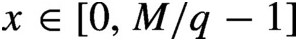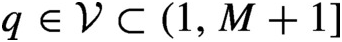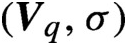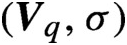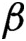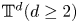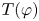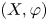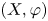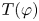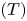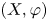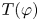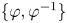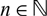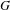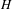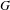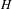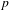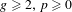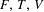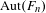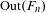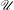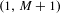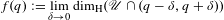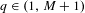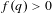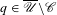Refine listing
Actions for selected content:
309 results in 37Bxx
On equicontinuous factors of flows on locally path-connected compact spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 3270-3287
- Print publication:
- November 2021
-
- Article
- Export citation
Complete regularity of Ellis semigroups of
 $\mathbb{Z} $-actions
$\mathbb{Z} $-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 3593-3609
- Print publication:
- December 2021
-
- Article
- Export citation
Asymptotically autonomous robustness of random attractors for a class of weakly dissipative stochastic wave equations on unbounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 1700-1730
- Print publication:
- December 2021
-
- Article
- Export citation
Number-theoretic positive entropy shifts with small centralizer and large normalizer
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2020, pp. 3201-3226
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
The set of points with Markovian symbolic dynamics for non-uniformly hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2020, pp. 3244-3269
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
Mean equicontinuity and mean sensitivity on cellular automata
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3704-3721
- Print publication:
- December 2021
-
- Article
- Export citation
Mixing properties of colourings of the ℤd lattice
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 360-373
-
- Article
- Export citation
On the rotation sets of generic homeomorphisms on the torus
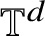 ${\mathbb T^d}$
${\mathbb T^d}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 07 October 2020, pp. 2983-3022
- Print publication:
- October 2021
-
- Article
- Export citation
Periodic points for amenable group actions on uniquely arcwise connected continua
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 30 September 2020, pp. 2833-2844
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
A context in which finite or unique ergodicity is generic
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 29 September 2020, pp. 3178-3200
- Print publication:
- October 2021
-
- Article
- Export citation
On the specification property and synchronization of unique q-expansions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2659-2705
- Print publication:
- September 2021
-
- Article
- Export citation
Continuous flows generate few homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 25 August 2020, pp. 971-983
-
- Article
- Export citation
Groups of piecewise linear homeomorphisms of flows
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1595-1622
- Print publication:
- August 2020
-
- Article
- Export citation
Variation of constants formula and exponential dichotomy for nonautonomous non-densely defined Cauchy problems
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 1347-1389
- Print publication:
- October 2021
-
- Article
- Export citation
DISTAL ACTIONS OF AUTOMORPHISMS OF NILPOTENT GROUPS G ON SUBG AND APPLICATIONS TO LATTICES IN LIE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 23 June 2020, pp. 343-362
- Print publication:
- May 2021
-
- Article
- Export citation
Symbolic dynamics in mean dimension theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 2542-2560
- Print publication:
- August 2021
-
- Article
- Export citation
MASS GROWTH OF OBJECTS AND CATEGORICAL ENTROPY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 04 June 2020, pp. 136-157
- Print publication:
- December 2021
-
- Article
- Export citation
Big mapping class groups and rigidity of the simple circle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 03 June 2020, pp. 1961-1987
- Print publication:
- July 2021
-
- Article
- Export citation
Divergence, undistortion and Hölder continuous cocycle superrigidity for full shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 2274-2293
- Print publication:
- August 2021
-
- Article
- Export citation
Relative bifurcation sets and the local dimension of univoque bases
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 2241-2273
- Print publication:
- August 2021
-
- Article
- Export citation