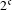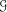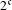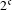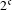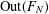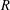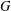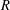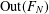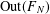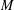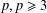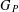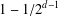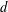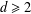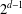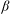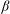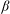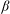Refine listing
Actions for selected content:
310 results in 37Bxx
Combinatorics of one-dimensional simple Toeplitz subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1673-1714
- Print publication:
- June 2020
-
- Article
- Export citation
LUSTERNIK–SCHNIRELMANN CATEGORY BASED ON THE DISCRETE CONLEY INDEX THEORY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 30 October 2018, pp. 693-704
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Characterizing asymptotic randomization in abelian cellular automata
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 25 September 2018, pp. 923-952
- Print publication:
- April 2020
-
- Article
- Export citation
A metric minimal PI cascade with
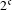 $2^{\mathfrak{c}}$minimal ideals
$2^{\mathfrak{c}}$minimal ideals
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 14 September 2018, pp. 1268-1281
- Print publication:
- May 2020
-
- Article
- Export citation
Pointwise Topological Stability
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 1179-1191
-
- Article
- Export citation
A NOTE ON ENTROPY OF AUTO-EQUIVALENCES: LOWER BOUND AND THE CASE OF ORBIFOLD PROJECTIVE LINES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 26 June 2018, pp. 86-103
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
COUNTING CONJUGACY CLASSES IN
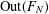 $\text{Out}(F_{N})$
$\text{Out}(F_{N})$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 412-421
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Visualizing Automorphisms of Graph Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 01 February 2018, pp. 215-249
-
- Article
- Export citation
ITERATED LOGARITHM SPEED OF RETURN TIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 04 October 2017, pp. 468-478
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
ON FUNCTIONS ATTRACTING POSITIVE ENTROPY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 69-79
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
STABLE, ALMOST STABLE AND ODD POINTS OF DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 245-255
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 11 April 2017, pp. 561-590
- Print publication:
- May 2019
-
- Article
- Export citation
TWO-SIDED SHIFT SPACES OVER INFINITE ALPHABETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 22 March 2017, pp. 357-386
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
ON THE EVENTUAL PERIODICITY OF PIECEWISE LINEAR CHAOTIC MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 16 February 2017, pp. 467-475
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
ON ANNULAR MAPS OF THE TORUS AND SUBLINEAR DIFFUSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 4 / September 2018
- Published online by Cambridge University Press:
- 23 June 2016, pp. 913-978
- Print publication:
- September 2018
-
- Article
- Export citation
Probabilistic cellular automata with general alphabets possessing a Markov chain as an invariant distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 369-391
- Print publication:
- June 2016
-
- Article
- Export citation
FINITELY CONSTRAINED GROUPS OF MAXIMAL HAUSDORFF DIMENSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 108-123
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
THE AUTOMORPHISM GROUP OF A SHIFT OF LINEAR GROWTH: BEYOND TRANSITIVITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 02 March 2015, e5
-
- Article
-
- You have access
- Open access
- Export citation
COHOMOLOGY OF THE PINWHEEL TILING
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 162-179
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
TOPOLOGICAL FULL GROUPS OF
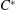 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^*$-ALGEBRAS ARISING FROM
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^*$-ALGEBRAS ARISING FROM 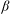 $\beta $-EXPANSIONS
$\beta $-EXPANSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 257-287
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation