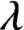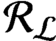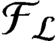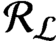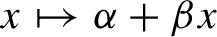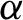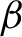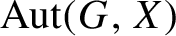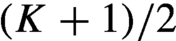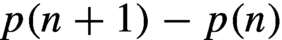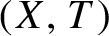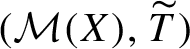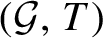Refine listing
Actions for selected content:
309 results in 37Bxx
Ahlfors regularity and fractal dimension of Smale spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 29 April 2021, pp. 2281-2332
- Print publication:
- July 2022
-
- Article
- Export citation
CELLULAR AUTOMATA OVER ALGEBRAIC STRUCTURES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 306-319
- Print publication:
- May 2022
-
- Article
- Export citation
Conley index for manifold-valued retarded functional differential equations without uniqueness of solutions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 19 April 2021, pp. 428-449
- Print publication:
- April 2022
-
- Article
- Export citation
Cantor spectrum for CMV and Jacobi matrices with coefficients arising from generalized skew-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2009-2027
- Print publication:
- June 2022
-
- Article
- Export citation
Generic chaos on dendrites
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 2108-2150
- Print publication:
- June 2022
-
- Article
- Export citation
Characteristic measures of symbolic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 1655-1661
- Print publication:
- May 2022
-
- Article
- Export citation
Subsystems of transitive subshifts with linear complexity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 17 March 2021, pp. 1967-1993
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
Prime number theorem for regular Toeplitz subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 1446-1473
- Print publication:
- April 2022
-
- Article
- Export citation
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS – ERRATUM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 2253-2255
- Print publication:
- November 2022
-
- Article
- Export citation
A variational principle for the metric mean dimension of free semigroup actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 01 February 2021, pp. 65-85
- Print publication:
- January 2022
-
- Article
- Export citation
 $\boldsymbol{C}^*$-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS
$\boldsymbol{C}^*$-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 230-263
- Print publication:
- April 2022
-
- Article
- Export citation
On subshifts with slow forbidden word growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 12 January 2021, pp. 1487-1516
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
Minimal flows with arbitrary centralizer
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 310-320
- Print publication:
- January 2022
-
- Article
- Export citation
The number of ergodic measures for transitive subshifts under the regular bispecial condition
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 86-140
- Print publication:
- January 2022
-
- Article
- Export citation
Uniformly positive entropy of induced transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 9-18
- Print publication:
- January 2022
-
- Article
- Export citation
Generic homeomorphisms have full metric mean dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 40-64
- Print publication:
- January 2022
-
- Article
- Export citation
Symbolic dynamics for non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2591-2658
- Print publication:
- September 2021
-
- Article
- Export citation
Balanced strong shift equivalence, balanced in-splits, and eventual conjugacy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 04 December 2020, pp. 19-39
- Print publication:
- January 2022
-
- Article
- Export citation
Expansive dynamics on locally compact groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 18 November 2020, pp. 3768-3779
- Print publication:
- December 2021
-
- Article
- Export citation
Kneading sequences for toy models of Hénon maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 3521-3540
- Print publication:
- December 2021
-
- Article
- Export citation
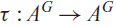
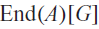
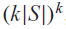
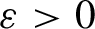
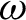
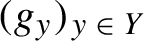
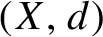
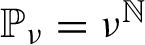
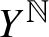
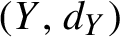
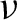

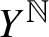
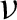
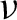

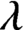

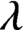
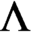
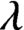
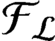
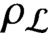
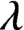
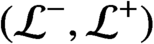

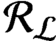
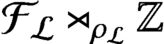 . It is a two-sided subshift analogue of asymptotic Ruelle algebras constructed from Smale spaces. If
. It is a two-sided subshift analogue of asymptotic Ruelle algebras constructed from Smale spaces. If