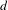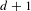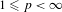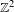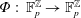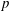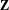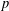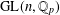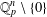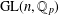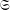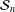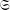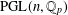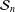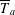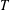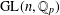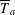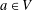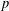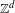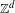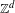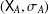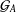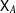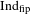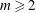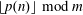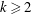Refine listing
Actions for selected content:
309 results in 37Bxx
The expressiveness of quasiperiodic and minimal shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1086-1138
- Print publication:
- April 2021
-
- Article
- Export citation
Lower bound for the Perron–Frobenius degrees of Perron numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1264-1280
- Print publication:
- April 2021
-
- Article
- Export citation
Shadowing and structural stability for operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 961-980
- Print publication:
- April 2021
-
- Article
- Export citation
On Baire measurable colorings of group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 818-845
- Print publication:
- March 2021
-
- Article
- Export citation
The Ellis semigroup of certain constant-length substitutions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 935-960
- Print publication:
- March 2021
-
- Article
- Export citation
Frequent universality criterion and densities
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 25 November 2019, pp. 846-868
- Print publication:
- March 2021
-
- Article
- Export citation
Support stability of maximizing measures for shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 09 October 2019, pp. 869-880
- Print publication:
- March 2021
-
- Article
- Export citation
Bounded complexity, mean equicontinuity and discrete spectrum
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 494-533
- Print publication:
- February 2021
-
- Article
- Export citation
Topological entropy of Markov set-valued functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 24 September 2019, pp. 321-337
- Print publication:
- February 2021
-
- Article
- Export citation
A switched server system semiconjugate to a minimal interval exchange
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 682-708
-
- Article
- Export citation
Automaticity and Invariant Measures of Linear Cellular Automata
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 1691-1726
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
The Category of Ordered Bratteli Diagrams
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 1-28
- Print publication:
- February 2021
-
- Article
- Export citation
Distributional chaos in multifractal analysis, recurrence and transitivity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 27 August 2019, pp. 349-378
- Print publication:
- February 2021
-
- Article
- Export citation
A Tits alternative for topological full groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 27 August 2019, pp. 622-640
- Print publication:
- February 2021
-
- Article
- Export citation
DISTALITY OF CERTAIN ACTIONS ON
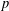 $p$-ADIC SPHERES
$p$-ADIC SPHERES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 250-261
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Directional dynamical cubes for minimal
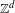 $\mathbb{Z}^{d}$-systems
$\mathbb{Z}^{d}$-systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 26 June 2019, pp. 3257-3295
- Print publication:
- December 2020
-
- Article
- Export citation
CUNTZ–KRIEGER ALGEBRAS AND ONE-SIDED CONJUGACY OF SHIFTS OF FINITE TYPE AND THEIR GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 21 June 2019, pp. 289-298
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Null systems in the non-minimal case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 17 June 2019, pp. 3420-3437
- Print publication:
- December 2020
-
- Article
- Export citation
Automatic Sequences and Generalised Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 13 June 2019, pp. 392-426
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
The Hausdorff dimension of multiply Xiong chaotic sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 3056-3077
- Print publication:
- November 2020
-
- Article
- Export citation