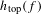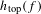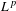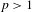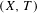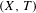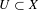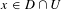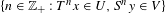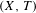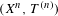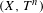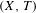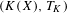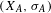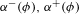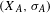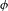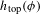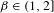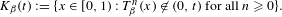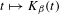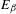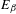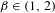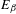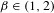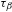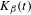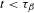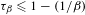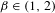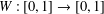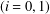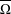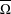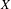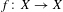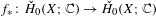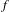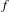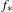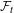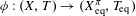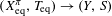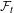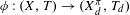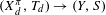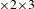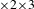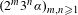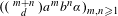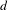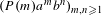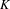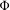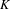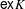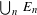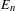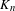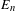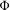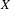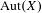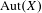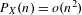Refine listing
Actions for selected content:
309 results in 37Bxx
HOMOLOGY AND MATUI’S HK CONJECTURE FOR GROUPOIDS ON ONE-DIMENSIONAL SOLENOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 105-117
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Smoothness of topological equivalence on the half line for nonautonomous systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 2484-2502
- Print publication:
- October 2020
-
- Article
- Export citation
Constant slope, entropy, and horseshoes for a map on a tame graph
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 22 April 2019, pp. 2970-2994
- Print publication:
- November 2020
-
- Article
- Export citation
Nilsystems and ergodic averages along primes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 11 April 2019, pp. 2769-2777
- Print publication:
- October 2020
-
- Article
-
- You have access
- Open access
- Export citation
An answer to Furstenberg’s problem on topological disjointness
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 10 April 2019, pp. 2467-2481
- Print publication:
- September 2020
-
- Article
- Export citation
On nilspace systems and their morphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 10 April 2019, pp. 3015-3029
- Print publication:
- November 2020
-
- Article
- Export citation
SIMPLICITY OF CROSSED PRODUCTS BY TWISTED PARTIAL ACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 202-225
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Automorphisms of the shift: Lyapunov exponents, entropy, and the dimension representation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2552-2570
- Print publication:
- September 2020
-
- Article
- Export citation
The
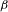 $\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
$\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2482-2514
- Print publication:
- September 2020
-
- Article
-
- You have access
- Open access
- Export citation
SYMMETRIC ITINERARY SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 06 March 2019, pp. 97-108
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Deviations in the Franks–Misiurewicz conjecture
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 2533-2540
- Print publication:
- September 2020
-
- Article
- Export citation
Topological and almost Borel universality for systems with the weak specification property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 2098-2115
- Print publication:
- August 2020
-
- Article
- Export citation
ON GENERATORS AND DISTURBANCES OF DYNAMICAL SYSTEMS IN THE CONTEXT OF CHAOTIC POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 76-85
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Dynamics and eigenvalues in dimension zero
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 04 January 2019, pp. 2434-2452
- Print publication:
- September 2020
-
- Article
- Export citation
Relativization of sensitivity in minimal systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1715-1728
- Print publication:
- June 2020
-
- Article
- Export citation
Autonomous and non-autonomous unbounded attractors under perturbations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 877-903
- Print publication:
- August 2019
-
- Article
- Export citation
A polynomial-exponential variation of Furstenberg’s
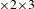 $\times 2\times 3$ theorem
$\times 2\times 3$ theorem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1729-1737
- Print publication:
- July 2020
-
- Article
- Export citation
Zero-dimensional isomorphic dynamical models
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 11 December 2018, pp. 2116-2130
- Print publication:
- August 2020
-
- Article
- Export citation
The automorphism group of a shift of slow growth is amenable
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 11 December 2018, pp. 1788-1804
- Print publication:
- July 2020
-
- Article
-
- You have access
- Export citation
Combinatorics of one-dimensional simple Toeplitz subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1673-1714
- Print publication:
- June 2020
-
- Article
- Export citation