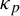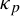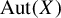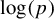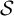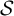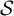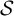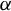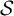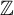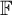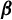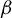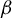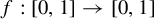Refine listing
Actions for selected content:
309 results in 37Bxx
Chaotic behavior of the p-adic Potts–Bethe mapping II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3433-3457
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Glider automata on all transitive sofic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3716-3744
- Print publication:
- December 2022
-
- Article
- Export citation
ORDERS OF GROWTH AND GENERALIZED ENTROPY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 28 September 2021, pp. 1581-1613
- Print publication:
- July 2023
-
- Article
- Export citation
Non-negative integral matrices with given spectral radius and controlled dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 3246-3269
- Print publication:
- October 2022
-
- Article
- Export citation
Reconstructing a minimal topological dynamical system from a set of return times
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 03 September 2021, pp. 2723-2739
- Print publication:
- September 2022
-
- Article
- Export citation
Soliton Decomposition of the Box-Ball System
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 03 September 2021, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reeb orbits that force topological entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 02 September 2021, pp. 3025-3068
- Print publication:
- October 2022
-
- Article
- Export citation
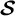 $\mathcal{\textbf{S}}$-adic characterization of minimal ternary dendric shifts
$\mathcal{\textbf{S}}$-adic characterization of minimal ternary dendric shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 02 September 2021, pp. 3393-3432
- Print publication:
- November 2022
-
- Article
- Export citation
A non-Borel special alpha-limit set in the square
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 22 July 2021, pp. 2550-2560
- Print publication:
- August 2022
-
- Article
- Export citation
Classification of backward filtrations and factor filtrations: examples from cellular automata
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 2890-2922
- Print publication:
- September 2022
-
- Article
- Export citation
Mixing rates for potentials of non-summable variations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 2823-2840
- Print publication:
- September 2022
-
- Article
- Export citation
On the automorphism group of minimal
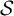 $\mathcal {S}$-adic subshifts of finite alphabet rank
$\mathcal {S}$-adic subshifts of finite alphabet rank
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 30 June 2021, pp. 2800-2822
- Print publication:
- September 2022
-
- Article
- Export citation
Unique ergodicity of the automorphism group of the semigeneric directed graph
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 28 June 2021, pp. 2561-2574
- Print publication:
- August 2022
-
- Article
- Export citation
A dichotomy for bounded displacement equivalence of Delone sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 18 June 2021, pp. 2693-2710
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- Export citation
On topological rank of factors of Cantor minimal systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 2866-2889
- Print publication:
- September 2022
-
- Article
- Export citation
On one-sided topological conjugacy of topological Markov shifts and gauge actions on Cuntz–Krieger algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 2575-2582
- Print publication:
- August 2022
-
- Article
- Export citation
New examples of Bernoulli algebraic actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 2923-2934
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- Export citation
Dynamic asymptotic dimension for actions of virtually cyclic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 364-372
-
- Article
- Export citation
Equilibrium measures of the natural extension of
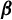 $\boldsymbol{\beta}$-shifts
$\boldsymbol{\beta}$-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2415-2430
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
A characterization of a map whose inverse limit is an arc
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2533-2549
- Print publication:
- August 2022
-
- Article
- Export citation