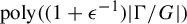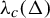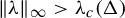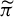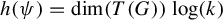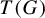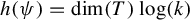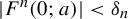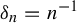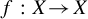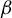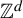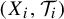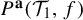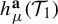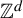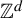Refine listing
Actions for selected content:
310 results in 37Bxx
Counting independent sets in amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 May 2023, pp. 958-1012
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable finiteness of twisted group rings and noisy linear cellular automata
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1089-1108
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper extensions of the 2-sphere’s conformal group present entropy and are 4-transitive
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 03 May 2023, pp. 1102-1122
- Print publication:
- April 2024
-
- Article
- Export citation
Binary factors of shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 888-932
- Print publication:
- March 2024
-
- Article
- Export citation
Entropy bounds for multi-word perturbations of subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 665-673
- Print publication:
- February 2024
-
- Article
- Export citation
Relative uniformly positive entropy of induced amenable group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 17 March 2023, pp. 569-593
- Print publication:
- February 2024
-
- Article
- Export citation
Dynamical properties of minimal Ferenczi subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 22 February 2023, pp. 3923-3970
- Print publication:
- December 2023
-
- Article
- Export citation
Sequence entropy tuples and mean sensitive tuples
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 February 2023, pp. 184-203
- Print publication:
- January 2024
-
- Article
- Export citation
Almost proximal extensions of minimal flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 4041-4073
- Print publication:
- December 2023
-
- Article
- Export citation
Recognizability of morphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 3578-3602
- Print publication:
- November 2023
-
- Article
- Export citation
Model sets with Euclidean internal space
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 3897-3922
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The topological entropy of powers on Lie groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 3726-3744
- Print publication:
- November 2023
-
- Article
- Export citation
A characterization of Thurston’s Master Teapot
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 10 November 2022, pp. 3354-3382
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical recurrence in the real quadratic family
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 3255-3287
- Print publication:
- October 2023
-
- Article
- Export citation
The structure of pointwise recurrent expansive homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 3448-3459
- Print publication:
- October 2023
-
- Article
- Export citation
Periodic expansion of one by Salem numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 14 October 2022, pp. 2841-2862
- Print publication:
- September 2023
-
- Article
- Export citation
QUASICONTINUITY, NONATTRACTING POINTS, DISTRIBUTIVE CHAOS AND RESISTANCE TO DISRUPTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 102-111
- Print publication:
- February 2023
-
- Article
- Export citation
A variational principle for weighted topological pressure under
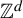 $\mathbb {Z}^{d}$-actions
$\mathbb {Z}^{d}$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 3311-3340
- Print publication:
- October 2023
-
- Article
- Export citation
Flip signatures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 3413-3447
- Print publication:
- October 2023
-
- Article
- Export citation
On conjugacy of natural extensions of one-dimensional maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 2915-2937
- Print publication:
- September 2023
-
- Article
- Export citation