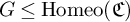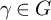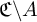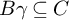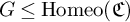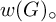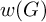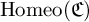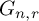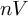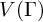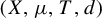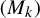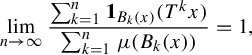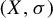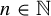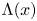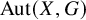Refine listing
Actions for selected content:
310 results in 37Bxx
Decidability of the isomorphism problem between multidimensional substitutive subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2054-2094
- Print publication:
- July 2025
-
- Article
- Export citation
The socle of subshift algebras, with applications to subshift conjugacy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-26
-
- Article
- Export citation
Intersective sets for sparse sets of integers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1370-1402
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological and metric emergence of continuous maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 27 December 2024, pp. 525-551
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Piecewise contractions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 1503-1540
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective dynamical systems beyond dimension zero and factors of SFTs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1329-1369
- Print publication:
- May 2025
-
- Article
- Export citation
Construction of smooth isomorphic and finite-to-one extensions of irrational rotations which are not almost automorphic
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1224-1245
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUFFICIENT CONDITIONS FOR A GROUP OF HOMEOMORPHISMS OF THE CANTOR SET TO BE TWO-GENERATED
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 2825-2858
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A recurrence-type strong Borel–Cantelli lemma for Axiom A diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 936-955
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On transversal Hölder regularity for flat Wieler solenoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 294-320
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal and proximal examples of
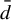 $\bar {d}$-stable and
$\bar {d}$-stable and 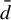 $\bar {d}$-approachable shift spaces
$\bar {d}$-approachable shift spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 396-426
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symbolic dynamics for pointwise hyperbolic systems on open regions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 595-648
- Print publication:
- February 2025
-
- Article
- Export citation
Multiplication cubes and multiplication automata
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 526-565
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibrium measures for two-sided shift spaces via dimension theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 427-466
- Print publication:
- February 2025
-
- Article
- Export citation
Subshifts of finite symbolic rank
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 807-848
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal zero entropy subshifts can be unrestricted along any sparse set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 566-572
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Indistinguishable asymptotic pairs and multidimensional Sturmian configurations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 31 May 2024, pp. 337-395
- Print publication:
- February 2025
-
- Article
- Export citation
On a class of self-similar sets which contain finitely many common points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
- Export citation
Minimal subdynamics and minimal flows without characteristic measures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relationships between two linearizations of the box-ball system: Kerov–Kirillov–Reschetikhin bijection and slot configuration
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation