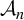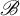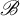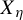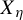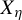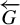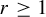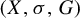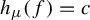Refine listing
Actions for selected content:
310 results in 37Bxx
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 May 2024, pp. 34-70
- Print publication:
- January 2025
-
- Article
- Export citation
Similarities and differences between specification and non-uniform specification
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 3501-3529
- Print publication:
- December 2024
-
- Article
- Export citation
Substreetutions and more on trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 2399-2453
- Print publication:
- September 2024
-
- Article
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 2647-2711
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measure transfer and S-adic developments for subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 3120-3154
- Print publication:
- November 2024
-
- Article
- Export citation
Invariant measures for
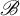 $\mathscr {B}$-free systems revisited
$\mathscr {B}$-free systems revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 2901-2932
- Print publication:
- October 2024
-
- Article
- Export citation
On the Ziv–Merhav theorem beyond Markovianity I
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 891-915
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An embedding theorem for subshifts over amenable groups with the comparison property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3155-3185
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures of Toeplitz subshifts on non-amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 3186-3215
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shifts of finite type on locally finite groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 3565-3598
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measures of maximal entropy of bounded density shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 20 February 2024, pp. 2960-2974
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant sets and nilpotency of endomorphisms of algebraic sofic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2859-2900
- Print publication:
- October 2024
-
- Article
- Export citation
Sufficient conditions for non-zero entropy of closed relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 3091-3119
- Print publication:
- November 2024
-
- Article
- Export citation
BRATTELI–VERSHIKISABILITY OF POLYGONAL BILLIARDS ON THE HYPERBOLIC PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 85-104
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures for substitutions on countable alphabets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2533-2564
- Print publication:
- September 2024
-
- Article
- Export citation
Topological stability for homeomorphisms with global attractor
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 493-503
- Print publication:
- June 2024
-
- Article
- Export citation
Conditional intermediate entropy and Birkhoff average properties of hyperbolic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 2257-2288
- Print publication:
- August 2024
-
- Article
- Export citation
Stabilized automorphism group of odometers and of Toeplitz subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 2289-2307
- Print publication:
- August 2024
-
- Article
- Export citation
Markov capacity for factor codes with an unambiguous symbol
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 07 November 2023, pp. 2199-2228
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A mechanism for ejecting a horseshoe from a partially hyperbolic chain recurrence class
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 2080-2142
- Print publication:
- August 2024
-
- Article
- Export citation