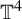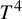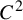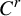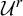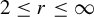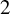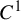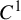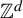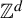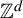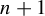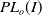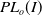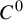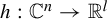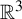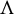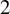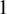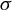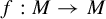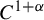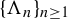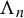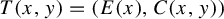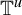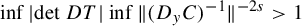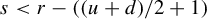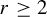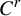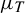Refine listing
Actions for selected content:
242 results in 37Cxx
Shub’s example revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 23 September 2024, pp. 894-914
- Print publication:
- March 2025
-
- Article
- Export citation
Multifractal analysis of homological growth rates for hyperbolic surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 849-883
- Print publication:
- March 2025
-
- Article
- Export citation
Symbolic dynamics for pointwise hyperbolic systems on open regions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 595-648
- Print publication:
- February 2025
-
- Article
- Export citation
Equilibrium measures for two-sided shift spaces via dimension theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 427-466
- Print publication:
- February 2025
-
- Article
- Export citation
Non-rigidity of partially hyperbolic abelian
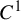 $C^1$-actions on tori
$C^1$-actions on tori
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 573-594
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bishop–Jones’ theorem and the ergodic limit set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 704-718
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Indistinguishable asymptotic pairs and multidimensional Sturmian configurations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 31 May 2024, pp. 337-395
- Print publication:
- February 2025
-
- Article
- Export citation
Distribution in homology classes and discrete fractal dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partially hyperbolic endomorphisms with expanding linear part
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 28 May 2024, pp. 321-336
- Print publication:
- February 2025
-
- Article
- Export citation
Girth Alternative for subgroups of
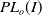 $PL_o(I)$
$PL_o(I)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-10
- Print publication:
- January 2025
-
- Article
- Export citation
Non-invertible planar self-affine sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. 49-65
- Print publication:
- July 2024
-
- Article
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 May 2024, pp. 34-70
- Print publication:
- January 2025
-
- Article
- Export citation
Similarities and differences between specification and non-uniform specification
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 3501-3529
- Print publication:
- December 2024
-
- Article
- Export citation
On the Hausdorff dimension of invariant measures of piecewise smooth circle homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 3599-3629
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Density of mode-locking property for quasi-periodically forced Arnold circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 04 April 2024, pp. 3645-3680
- Print publication:
- December 2024
-
- Article
- Export citation
Scale recurrence lemma and dimension formula for Cantor sets in the complex plane
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 25 March 2024, pp. 3316-3357
- Print publication:
- November 2024
-
- Article
- Export citation
Upper, down, two-sided Lorenz attractor, collisions, merging, and switching
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 21 February 2024, pp. 2737-2781
- Print publication:
- October 2024
-
- Article
- Export citation
Dimension estimates and approximation in non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 2975-3001
- Print publication:
- October 2024
-
- Article
- Export citation
Regularity and linear response formula of the SRB measures for solenoidal attractors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 06 February 2024, pp. 2782-2831
- Print publication:
- October 2024
-
- Article
- Export citation
Equilibrium states for non-uniformly expanding skew products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2599-2620
- Print publication:
- September 2024
-
- Article
- Export citation