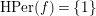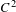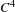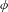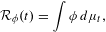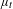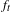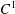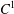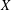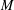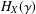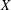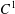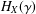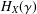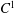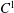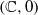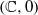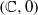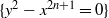Refine listing
Actions for selected content:
242 results in 37Cxx
HOMOTOPY MINIMAL PERIODS FOR HYPERBOLIC MAPS ON INFRA-NILMANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 1-18
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
STABLE, ALMOST STABLE AND ODD POINTS OF DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 245-255
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
NON-UNIFORM TRICHOTOMIES AND ARBITRARY GROWTH RATES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 03 April 2017, pp. 518-537
- Print publication:
- 2017
-
- Article
- Export citation
CONTINUITY OF THE HAUSDORFF DIMENSION FOR GRAPH-DIRECTED SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 471-478
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
CENTRAL LIMIT THEOREM FOR THE MODULUS OF CONTINUITY OF AVERAGES OF OBSERVABLES ON TRANSVERSAL FAMILIES OF PIECEWISE EXPANDING UNIMODAL MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 13 July 2016, pp. 673-733
- Print publication:
- June 2018
-
- Article
- Export citation
Semidefinite Optimization Estimating Bounds on Linear Functionals Defined on Solutions of Linear ODEs
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 599-615
- Print publication:
- August 2016
-
- Article
- Export citation
A Computational Study of a Data Assimilation Algorithm for the Two-dimensional Navier-Stokes Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 1094-1110
- Print publication:
- April 2016
-
- Article
- Export citation
ORBITALLY NONEXPANSIVE MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 497-503
- Print publication:
- June 2016
-
- Article
-
- You have access
- Open access
- Export citation
METASTABLE SETS IN OPEN DYNAMICAL SYSTEMS AND SUBSTOCHASTIC MARKOV CHAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 344-345
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
CENTER MANIFOLDS FOR PARTIALLY HYPERBOLIC SETS WITHOUT STRONG UNSTABLE CONNECTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 11 March 2015, pp. 785-828
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
ANALYTIC REDUCIBILITY OF RESONANT COCYCLES TO A NORMAL FORM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 27 November 2014, pp. 203-223
- Print publication:
- January 2016
-
- Article
- Export citation
HYPERBOLICITY OF HOMOCLINIC CLASSES OF
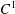 $C^{1}$ VECTOR FIELDS
$C^{1}$ VECTOR FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 375-389
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Sur les rapprochements par conjugaison en dimension 1 et classe
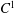 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 19 June 2014, pp. 1183-1195
- Print publication:
- July 2014
-
- Article
- Export citation
CLASSIFICATION OF SYMMETRY GROUPS FOR PLANAR
 $n$ -BODY CHOREOGRAPHIES
$n$ -BODY CHOREOGRAPHIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 13 December 2013, e5
-
- Article
-
- You have access
- Open access
- Export citation
Cyclic stabilizers and infinitely many hyperbolic orbits for pseudogroups on
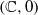 $( \mathbb{C} , 0)$
$( \mathbb{C} , 0)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 06 August 2013, pp. 413-446
- Print publication:
- April 2014
-
- Article
- Export citation
Generic pseudogroups on
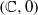 $( \mathbb{C} , 0)$ and the topology of leaves
$( \mathbb{C} , 0)$ and the topology of leaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 01 July 2013, pp. 1401-1430
- Print publication:
- August 2013
-
- Article
- Export citation
THE CONLEY ATTRACTORS OF AN ITERATED FUNCTION SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 267-279
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Conjugacies for impulsive equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 01 November 2011, pp. 65-78
-
- Article
-
- You have access
- Export citation
Pairs of periodic orbits with fixed homology difference
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 799-808
-
- Article
-
- You have access
- Export citation
Caractérisation des exemples de Lattès et de Kummer
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1235-1270
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation