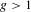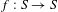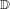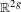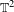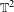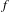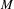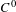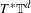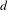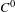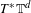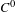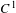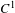Refine listing
Actions for selected content:
241 results in 37Cxx
Sobolev regularity of solutions of the cohomological equation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 685-789
- Print publication:
- March 2021
-
- Article
- Export citation
Assouad Spectrum Thresholds for Some Random Constructions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 434-453
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
An example of a planar Anosov diffeomorphism without fixed points
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 923-934
- Print publication:
- March 2021
-
- Article
- Export citation
Lower Assouad Dimension of Measures and Regularity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 22 November 2019, pp. 379-415
- Print publication:
- March 2021
-
- Article
- Export citation
There are no proper topological hyperbolic homoclinic classes for area-preserving maps
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 12 November 2019, pp. 217-228
-
- Article
- Export citation
A condition that implies full homotopical complexity of orbits for surface homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 24 September 2019, pp. 1-47
- Print publication:
- January 2021
-
- Article
- Export citation
Partially hyperbolic surface endomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 272-282
- Print publication:
- January 2021
-
- Article
- Export citation
The numbers of periodic orbits hidden at fixed points of holomorphic maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 578-592
- Print publication:
- February 2021
-
- Article
- Export citation
Distributional chaos in multifractal analysis, recurrence and transitivity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 27 August 2019, pp. 349-378
- Print publication:
- February 2021
-
- Article
- Export citation
A Tits alternative for topological full groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 27 August 2019, pp. 622-640
- Print publication:
- February 2021
-
- Article
- Export citation
The
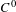 $C^{0}$ integrability of symplectic twist maps without conjugate points
$C^{0}$ integrability of symplectic twist maps without conjugate points
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 August 2019, pp. 48-65
- Print publication:
- January 2021
-
- Article
- Export citation
Global fixed points for nilpotent actions on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3339-3367
- Print publication:
- December 2020
-
- Article
- Export citation
Skew product Smale endomorphisms over countable shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 25 June 2019, pp. 3105-3149
- Print publication:
- November 2020
-
- Article
- Export citation
Smoothness of topological equivalence on the half line for nonautonomous systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 2484-2502
- Print publication:
- October 2020
-
- Article
- Export citation
SIMPLICITY OF CROSSED PRODUCTS BY TWISTED PARTIAL ACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 202-225
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
STABLE SETS OF CERTAIN NON-UNIFORMLY HYPERBOLIC HORSESHOES HAVE THE EXPECTED DIMENSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 04 April 2019, pp. 305-329
- Print publication:
- January 2021
-
- Article
- Export citation
Lyapunov optimization for non-generic one-dimensional expanding Markov maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2571-2592
- Print publication:
- September 2020
-
- Article
- Export citation
Upper bounds on measure-theoretic tail entropy for dominated splittings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 2305-2316
- Print publication:
- September 2020
-
- Article
- Export citation
On–off intermittency and chaotic walks
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1805-1842
- Print publication:
- July 2020
-
- Article
-
- You have access
- Open access
- Export citation
NON-HYPERBOLIC ERGODIC MEASURES AND HORSESHOES IN PARTIALLY HYPERBOLIC HOMOCLINIC CLASSES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1765-1792
- Print publication:
- September 2020
-
- Article
- Export citation