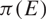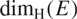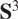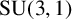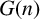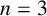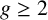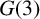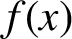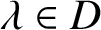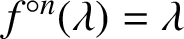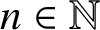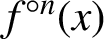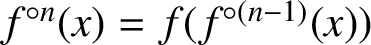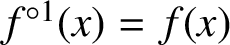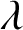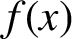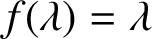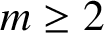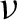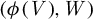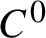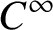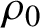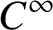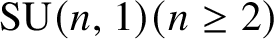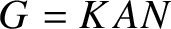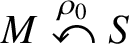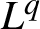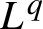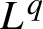Refine listing
Actions for selected content:
241 results in 37Cxx
Margulis–Ruelle inequality for general manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 2064-2079
- Print publication:
- June 2022
-
- Article
- Export citation
The essential coexistence phenomenon in Hamiltonian dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 592-613
- Print publication:
- February 2022
-
- Article
- Export citation
The bifurcation locus for numbers of bounded type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2239-2269
- Print publication:
- July 2022
-
- Article
- Export citation
Normal forms for strong magnetic systems on surfaces: trapping regions and rigidity of Zoll systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 March 2021, pp. 1871-1897
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
There are no deviations for the ergodic averages of Giulietti–Liverani horocycle flows on the two-torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 500-513
- Print publication:
- February 2022
-
- Article
- Export citation
Projections of Poisson cut-outs in the Heisenberg group and the visual 3-sphere
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 197-230
- Print publication:
- January 2022
-
- Article
- Export citation
LOCAL COORDINATES FOR COMPLEX AND QUATERNIONIC HYPERBOLIC PAIRS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 57-78
- Print publication:
- August 2022
-
- Article
- Export citation
FIXED POINTS OF POLYNOMIALS OVER DIVISION RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 01 March 2021, pp. 256-262
- Print publication:
- October 2021
-
- Article
- Export citation
Equivariant wrapped Floer homology and symmetric periodic Reeb orbits
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 February 2021, pp. 1708-1763
- Print publication:
- May 2022
-
- Article
- Export citation
A variational principle for the metric mean dimension of free semigroup actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 01 February 2021, pp. 65-85
- Print publication:
- January 2022
-
- Article
- Export citation
BOUNDNESS OF INTERSECTION NUMBERS FOR ACTIONS BY TWO-DIMENSIONAL BIHOLOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 1677-1700
- Print publication:
- September 2022
-
- Article
- Export citation
Realization of analytic moduli for parabolic Dulac germs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 195-249
- Print publication:
- January 2022
-
- Article
- Export citation
Generic homeomorphisms have full metric mean dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 40-64
- Print publication:
- January 2022
-
- Article
- Export citation
Diffeomorphism cocycles over partially hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 263-286
- Print publication:
- January 2022
-
- Article
- Export citation
Symbolic dynamics for non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2591-2658
- Print publication:
- September 2021
-
- Article
- Export citation
Steady Euler flows and Beltrami fields in high dimensions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 07 December 2020, pp. 3610-3633
- Print publication:
- December 2021
-
- Article
- Export citation
Dynamical incoherence for a large class of partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3227-3243
- Print publication:
- November 2021
-
- Article
- Export citation
Vanishing of cohomology and parameter rigidity of actions of solvable Lie groups, II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3023-3059
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Foliations and conjugacy, II: the Mendes conjecture for time-one maps of flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3307-3324
- Print publication:
- November 2021
-
- Article
- Export citation
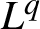 $L^{q}$-spectra of measures on planar non-conformal attractors
$L^{q}$-spectra of measures on planar non-conformal attractors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 3288-3306
- Print publication:
- November 2021
-
- Article
- Export citation