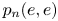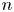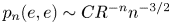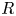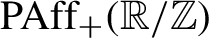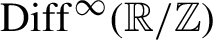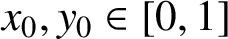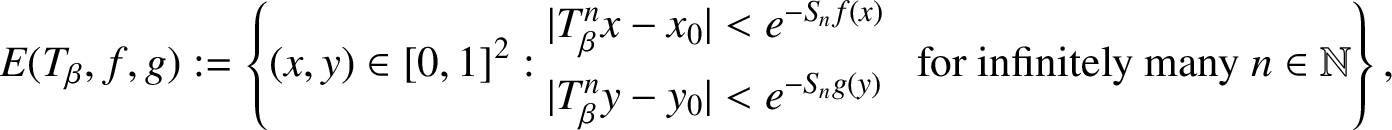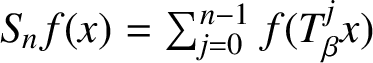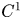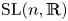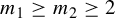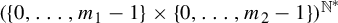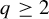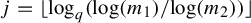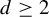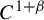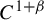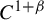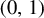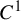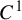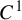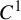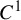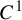Refine listing
Actions for selected content:
242 results in 37Cxx
Local limit theorems in relatively hyperbolic groups II: the non-spectrally degenerate case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 764-830
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost blenders and parablenders
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 24 March 2022, pp. 1087-1128
- Print publication:
- April 2023
-
- Article
- Export citation
Distortion in the group of circle homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 23 March 2022, pp. 1081-1086
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HIGHER-DIMENSIONAL SHRINKING TARGET PROBLEM FOR BETA DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 22 March 2022, pp. 289-311
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
C1 actions on manifolds by lattices in Lie groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 529-549
- Print publication:
- March 2022
-
- Article
- Export citation
New approach to weighted topological entropy and pressure
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 28 January 2022, pp. 1004-1034
- Print publication:
- March 2023
-
- Article
- Export citation
Dimensions of ‘self-affine sponges’ invariant under the action of multiplicative integers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 14 December 2021, pp. 417-459
- Print publication:
- February 2023
-
- Article
- Export citation
On the equidistribution of unstable curves for pseudo-Anosov diffeomorphisms of compact surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 855-880
- Print publication:
- March 2022
-
- Article
- Export citation
Typical properties of periodic Teichmüller geodesics: Lyapunov exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 17 November 2021, pp. 556-584
- Print publication:
- February 2023
-
- Article
- Export citation
On the accumulation of separatrices by invariant circles
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 17 November 2021, pp. 1057-1097
- Print publication:
- March 2022
-
- Article
- Export citation
The K-property for some unique equilibrium states in flows and homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 12 November 2021, pp. 2509-2532
- Print publication:
- August 2022
-
- Article
- Export citation
Exponential mixing of frame flows for convex cocompact hyperbolic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 08 November 2021, pp. 2585-2634
- Print publication:
- December 2021
-
- Article
- Export citation
S-limit shadowing is generic for continuous Lebesgue measure-preserving circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 25 October 2021, pp. 78-98
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted cohomological equations for translation flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 22 October 2021, pp. 881-916
- Print publication:
- March 2022
-
- Article
- Export citation
Flexibility of Lyapunov exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 554-591
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smoothness of stable holonomies inside center-stable manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3593-3618
- Print publication:
- December 2022
-
- Article
- Export citation
Quasisymmetric orbit-flexibility of multicritical circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3271-3310
- Print publication:
- November 2022
-
- Article
- Export citation
STATISTICAL STABILITY FOR DETERMINISTIC AND RANDOM DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 171-172
- Print publication:
- February 2022
-
- Article
-
- You have access
- HTML
- Export citation
ORDERS OF GROWTH AND GENERALIZED ENTROPY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 28 September 2021, pp. 1581-1613
- Print publication:
- July 2023
-
- Article
- Export citation
Dimension estimates for
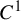 $C^1$ iterated function systems and repellers. Part II
$C^1$ iterated function systems and repellers. Part II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3357-3392
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation