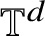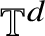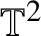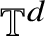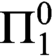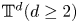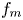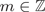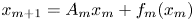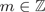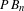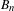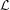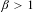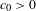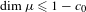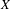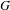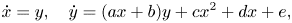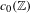Refine listing
Actions for selected content:
241 results in 37Cxx
The Assouad spectrum of random self-affine carpets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 15 October 2020, pp. 2927-2945
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
LINEAR RESPONSE IN DYNAMICAL SYSTEMS: OPTIMISATION AND FINITE-TIME COHERENT SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 October 2020, pp. 515-516
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
On the rotation sets of generic homeomorphisms on the torus
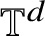 ${\mathbb T^d}$
${\mathbb T^d}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 07 October 2020, pp. 2983-3022
- Print publication:
- October 2021
-
- Article
- Export citation
GÖDEL DIFFEOMORPHISMS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 01 September 2020, pp. 219-223
- Print publication:
- December 2020
-
- Article
- Export citation
Continuous flows generate few homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 25 August 2020, pp. 971-983
-
- Article
- Export citation
Isolas of multi-pulse solutions to lattice dynamical systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 20 July 2020, pp. 916-952
- Print publication:
- June 2021
-
- Article
- Export citation
Shadowing for infinite dimensional dynamics and exponential trichotomies
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 June 2020, pp. 863-884
- Print publication:
- June 2021
-
- Article
- Export citation
STOCHASTIC POTENTIALS OF INTERMITTENT MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 18 June 2020, pp. 145-153
- Print publication:
- February 2021
-
- Article
- Export citation
Symbolic dynamics in mean dimension theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 2542-2560
- Print publication:
- August 2021
-
- Article
- Export citation
Non-realizability of the pure braid group as area-preserving homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 1988-1999
- Print publication:
- July 2021
-
- Article
- Export citation
Transfer operators for ultradifferentiable expanding maps of the circle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 2049-2068
- Print publication:
- July 2021
-
- Article
- Export citation
Smale endomorphisms over graph-directed Markov systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 2508-2541
- Print publication:
- August 2021
-
- Article
- Export citation
Big mapping class groups and rigidity of the simple circle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 03 June 2020, pp. 1961-1987
- Print publication:
- July 2021
-
- Article
- Export citation
Maximizing Bernoulli measures and dimension gaps for countable branched systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1921-1939
- Print publication:
- July 2021
-
- Article
- Export citation
Uniform convergence in von Neumann’s ergodic theorem in the absence of a spectral gap
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1601-1611
- Print publication:
- June 2021
-
- Article
- Export citation
Asymptotic escape rates and limiting distributions for multimodal maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 1656-1705
- Print publication:
- June 2021
-
- Article
- Export citation
Limit group invariants for non-free Cantor actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 1751-1794
- Print publication:
- June 2021
-
- Article
- Export citation
Phase portraits of the quadratic polynomial Liénard differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 202-216
- Print publication:
- February 2021
-
- Article
- Export citation
Statistical properties for compositions of standard maps with increasing coefficient
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 981-1024
- Print publication:
- April 2021
-
- Article
- Export citation
Shadowing and structural stability for operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 961-980
- Print publication:
- April 2021
-
- Article
- Export citation