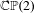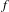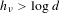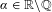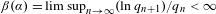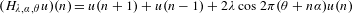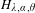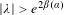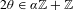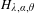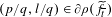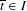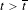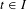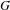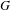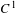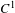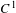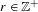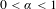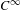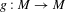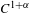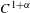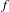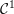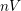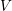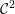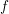Refine listing
Actions for selected content:
241 results in 37Cxx
Dimension of ergodic measures and currents on
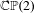 $\mathbb{C}\mathbb{P}(2)$
$\mathbb{C}\mathbb{P}(2)$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 04 January 2019, pp. 2131-2155
- Print publication:
- August 2020
-
- Article
- Export citation
Almost Mathieu operators with completely resonant phases
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1875-1893
- Print publication:
- July 2020
-
- Article
- Export citation
ON TYPICALITY OF TRANSLATION FLOWS WHICH ARE DISJOINT WITH THEIR INVERSE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 11 December 2018, pp. 1677-1737
- Print publication:
- September 2020
-
- Article
- Export citation
A consequence of the growth of rotation sets for families of diffeomorphisms of the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1441-1458
- Print publication:
- June 2020
-
- Article
- Export citation
Cogrowth for group actions with strongly contracting elements
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1738-1754
- Print publication:
- July 2020
-
- Article
- Export citation
Unique ergodicity of the horocycle flow on Riemannnian foliations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1459-1479
- Print publication:
- June 2020
-
- Article
- Export citation
The
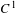 $C^{1}$ property of convex carrying simplices for competitive maps
$C^{1}$ property of convex carrying simplices for competitive maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1335-1350
- Print publication:
- May 2020
-
- Article
- Export citation
SRB measures for partially hyperbolic attractors of local diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1545-1593
- Print publication:
- June 2020
-
- Article
- Export citation
On the conservative pasting lemma
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1402-1440
- Print publication:
- May 2020
-
- Article
- Export citation
On the stable ergodicity of Berger–Carrasco’s example
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1008-1056
- Print publication:
- April 2020
-
- Article
- Export citation
Simultaneous dense and non-dense orbits for certain partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 04 September 2018, pp. 1083-1107
- Print publication:
- April 2020
-
- Article
- Export citation
Pointwise Topological Stability
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 1179-1191
-
- Article
- Export citation
DYNAMIC ISOPERIMETRY ON GRAPHS AND WEIGHTED RIEMANNIAN MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 514-515
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Optimal stability estimates for continuity equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 16 July 2018, pp. 1279-1296
- Print publication:
- December 2018
-
- Article
- Export citation
Diffeomorphism groups of tame Cantor sets and Thompson-like groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1066-1110
- Print publication:
- May 2018
-
- Article
- Export citation
DYNAMIC RELATIONSHIP BETWEEN THE MUTUAL INTERFERENCE AND GESTATION DELAYS OF A HYBRID TRITROPHIC FOOD CHAIN MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 3 / January 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 370-401
-
- Article
-
- You have access
- Export citation
Recurrence to Shrinking Targets on Typical Self-Affine Fractals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 387-400
-
- Article
- Export citation
Local Fractal Interpolation on Unbounded Domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 January 2018, pp. 151-167
-
- Article
- Export citation
LOWER BOUNDS ALONG STABLE MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 02 October 2017, pp. 527-537
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
HOMOTOPY MINIMAL PERIODS FOR HYPERBOLIC MAPS ON INFRA-NILMANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 1-18
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation