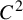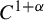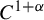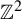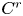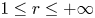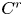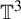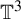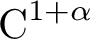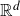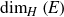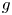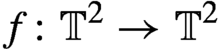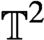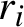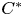Refine listing
Actions for selected content:
242 results in 37Cxx
Examples of distorted interval diffeomorphisms of intermediate regularity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3311-3324
- Print publication:
- November 2022
-
- Article
- Export citation
Geodesic stretch, pressure metric and marked length spectrum rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 09 August 2021, pp. 974-1022
- Print publication:
- March 2022
-
- Article
- Export citation
Transversal local rigidity of discrete abelian actions on Heisenberg nilmanifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 04 August 2021, pp. 3111-3151
- Print publication:
- October 2022
-
- Article
- Export citation
Fast growth of the number of periodic points arising from heterodimensional connections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 1899-1963
- Print publication:
- September 2021
-
- Article
- Export citation
Centralizers of derived-from-Anosov systems on
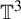 ${\mathbb T}^3$: rigidity versus triviality
${\mathbb T}^3$: rigidity versus triviality
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 02 August 2021, pp. 2841-2865
- Print publication:
- September 2022
-
- Article
- Export citation
GEOMETRICAL AND MEASURE-THEORETIC STRUCTURES OF MAPS WITH A MOSTLY EXPANDING CENTER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 July 2021, pp. 919-959
- Print publication:
- March 2023
-
- Article
- Export citation
Random fractals and their intersection with winning sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 07 July 2021, pp. 655-684
- Print publication:
- May 2022
-
- Article
- Export citation
Parrondo's paradox for homoeomorphisms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 16 June 2021, pp. 817-825
- Print publication:
- August 2022
-
- Article
- Export citation
A new proof of the dimension gap for the Gauss map
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 43-71
- Print publication:
- January 2022
-
- Article
- Export citation
BEYOND SLOW-FAST: RELAXATION OSCILLATIONS IN SINGULARLY PERTURBED NONSMOOTH SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 342-343
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
Almost existence from the feral perspective and some questions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 792-834
- Print publication:
- February 2022
-
- Article
- Export citation
Smooth, mixing transformations with loosely Bernoulli Cartesian square
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1252-1283
- Print publication:
- March 2022
-
- Article
- Export citation
Turnpike in infinite dimension
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 416-430
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flexibility of Lyapunov exponents with respect to two classes of measures on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 737-776
- Print publication:
- February 2022
-
- Article
- Export citation
Lyapunov exponent of random dynamical systems on the circle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 2080-2107
- Print publication:
- June 2022
-
- Article
- Export citation
Absolute continuity, Lyapunov exponents, and rigidity II: systems with compact center leaves
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 437-490
- Print publication:
- February 2022
-
- Article
- Export citation
Dynamic aspects of tumour–immune system interaction under a periodic immunotherapy
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 606-645
-
- Article
- Export citation
Thermodynamics of smooth models of pseudo–Anosov homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 1284-1326
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- Export citation
Accessibility and centralizers for partially hyperbolic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 835-854
- Print publication:
- March 2022
-
- Article
- Export citation
Dynamic asymptotic dimension for actions of virtually cyclic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 364-372
-
- Article
- Export citation