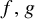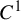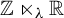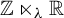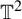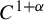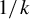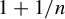Refine listing
Actions for selected content:
242 results in 37Cxx
GENERIC PLANAR PHASE RESETTING NEAR A PHASELESS POINT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modulus of continuity of invariant densities and entropies for piecewise expanding maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 2976-2991
- Print publication:
- October 2025
-
- Article
- Export citation
All, most, some? On diffeomorphisms of the interval that are distorted and/or conjugate to powers of themselves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 909-944
-
- Article
- Export citation
Two dynamical approaches to the notion of exponential separation for random systems of delay differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED RUELLE ZETA FUNCTION ON HYPERBOLIC MANIFOLDS AND COMPLEX-VALUED ANALYTIC TORSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 813-845
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hölder continuity of measures for heavy tail potentials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 2476-2513
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for equilibrium states on amenable group subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 2414-2438
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
First Ruelle resonance for an Anosov flow with smooth potential
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2439-2475
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New classes of quasigeodesic Anosov flows in
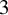 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2095-2131
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shadowing and hyperbolicity for linear delay difference equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-30
-
- Article
- Export citation
Minimal strong foliations in skew-products of iterated function systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 2273-2313
- Print publication:
- August 2025
-
- Article
- Export citation
Integrability of special quadratic systems with invariant hyperbolas
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-27
-
- Article
- Export citation
Finite data rigidity for one-dimensional expanding maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1597-1618
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological and metric emergence of continuous maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 27 December 2024, pp. 525-551
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Piecewise contractions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 1503-1540
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global rigidity of smooth
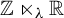 ${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on
${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on  ${\mathbb{T}}^{2}$
${\mathbb{T}}^{2}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 1161-1176
- Print publication:
- April 2025
-
- Article
- Export citation
Geometric properties of disintegration of measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1619-1648
- Print publication:
- May 2025
-
- Article
- Export citation
Construction of smooth isomorphic and finite-to-one extensions of irrational rotations which are not almost automorphic
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1224-1245
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Birkhoff attractors of dissipative billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 989-1047
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the critical regularity of nilpotent groups acting on the interval: the metabelian case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1177-1198
- Print publication:
- April 2025
-
- Article
- Export citation