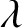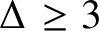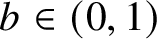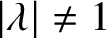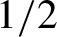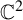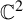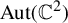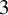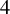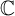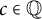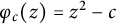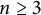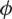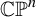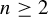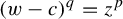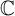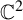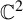Refine listing
Actions for selected content:
126 results in 37Fxx
Lee–Yang zeros and the complexity of the ferromagnetic Ising model on bounded-degree graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 07 February 2022, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff dimension of escaping sets of meromorphic functions II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 1471-1491
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Circle packings, kissing reflection groups and critically fixed anti-rational maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 17 January 2022, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant escaping Fatou components with two rank-one limit functions for automorphisms of
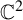 ${\mathbb C}^2$
${\mathbb C}^2$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 22 November 2021, pp. 401-416
- Print publication:
- February 2023
-
- Article
- Export citation
Julia sets of Zorich maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 692-728
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable intersections of conformal Cantor sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 25 October 2021, pp. 1-49
- Print publication:
- January 2023
-
- Article
- Export citation
Slices of parameter space for meromorphic maps with two asymptotic values
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 99-139
- Print publication:
- January 2023
-
- Article
- Export citation
Dynamical degrees of affine-triangular automorphisms of affine spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 3551-3592
- Print publication:
- December 2022
-
- Article
- Export citation
Homotopy Hubbard trees for post-singularly finite exponential maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 01 October 2021, pp. 253-298
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some results on the Flynn–Poonen–Schaefer conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 August 2021, pp. 598-611
- Print publication:
- September 2022
-
- Article
- Export citation
Generalizations of Douady’s magic formula
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 28 July 2021, pp. 2784-2799
- Print publication:
- September 2022
-
- Article
- Export citation
Permutable quasiregular maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 105-121
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Periodic points of post-critically algebraic holomorphic endomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 2382-2414
- Print publication:
- July 2022
-
- Article
- Export citation
Dynamics of hyperbolic correspondences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2661-2692
- Print publication:
- August 2022
-
- Article
- Export citation
Topological and geometric hyperbolicity criteria for polynomial automorphisms of
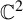 ${\mathbb {C}^2}$
${\mathbb {C}^2}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2151-2171
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Lee-Yang zeros of the antiferromagnetic Ising model
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2172-2206
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
On the dimension of points which escape to infinity at given rate under exponential iteration
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 29 March 2021, pp. 1591-1623
- Print publication:
- May 2022
-
- Article
- Export citation
Total disconnectedness of Julia sets of random quadratic polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1764-1780
- Print publication:
- May 2022
-
- Article
- Export citation
Orbifold expansion and entire functions with bounded Fatou components
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1807-1846
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Topological characterisation of rational maps with Siegel disks
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 10 February 2021, pp. 1-41
- Print publication:
- January 2022
-
- Article
- Export citation