Refine listing
Actions for selected content:
126 results in 37Fxx
Hausdorff Dimension of Sets of Escaping Points and Escaping Parameters for Elliptic Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 30 December 2015, pp. 671-690
-
- Article
- Export citation
Optimal cycles in ultrametric dynamics and minimally ramified power series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 187-222
- Print publication:
- January 2016
-
- Article
- Export citation
CHAINS OF FUNCTIONS IN
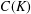 $C(K)$-SPACES
$C(K)$-SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 350-363
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
SHRINKING TARGETS FOR NONAUTONOMOUS DYNAMICAL SYSTEMS CORRESPONDING TO CANTOR SERIES EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 205-213
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Gaussian Random Particles with Flexible Hausdorff Dimension
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 307-327
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
ON THE ESCAPING SET OF MEROMORPHIC FUNCTIONS WITH DIRECT TRACTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 68-76
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
The M-set of λ exp(z)/z has infinite area
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 133-159
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
A GEOMETRIC STUDY OF WASSERSTEIN SPACES: ULTRAMETRICS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 27 May 2014, pp. 162-178
- Print publication:
- January 2015
-
- Article
- Export citation
DEGENERATIONS OF COMPLEX DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 April 2014, e6
-
- Article
-
- You have access
- Open access
- Export citation
SPECIAL CURVES AND POSTCRITICALLY FINITE POLYNOMIALS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 19 September 2013, e3
-
- Article
-
- You have access
- Open access
- Export citation
Cyclic stabilizers and infinitely many hyperbolic orbits for pseudogroups on
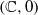 $( \mathbb{C} , 0)$
$( \mathbb{C} , 0)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 06 August 2013, pp. 413-446
- Print publication:
- April 2014
-
- Article
- Export citation
Generic pseudogroups on
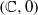 $( \mathbb{C} , 0)$ and the topology of leaves
$( \mathbb{C} , 0)$ and the topology of leaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 01 July 2013, pp. 1401-1430
- Print publication:
- August 2013
-
- Article
- Export citation
ON THE UNIFORM PERFECTNESS OF THE BOUNDARY OF MULTIPLY CONNECTED WANDERING DOMAINS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 04 November 2011, pp. 289-311
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
HOLOMORPHIC FLOWS WITH PERIODIC ORBITS ON STEIN SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 177-186
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
A gap principle for dynamics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 1056-1072
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Characteristic foliation on a hypersurface of general type in a projective symplectic manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 497-506
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
RATIONAL MAPS ADMITTING MEROMORPHIC INVARIANT LINE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 13 August 2009, pp. 454-461
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
CHEBYSHEV POLYNOMIALS ON JULIA SETS AND EQUIPOTENTIAL CURVES FOR THE FAMILY P(z)=zd−c
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 279-287
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
CONSTRUCTING HERMAN RINGS BY TWISTING ANNULUS HOMEOMORPHISMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 139-143
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
Caractérisation des exemples de Lattès et de Kummer
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1235-1270
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
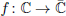 be a non-constant elliptic function. We prove that the Hausdorff dimension of the escaping set of
be a non-constant elliptic function. We prove that the Hausdorff dimension of the escaping set of 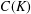
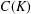
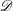
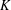
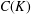
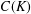
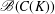
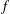
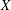
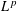
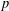
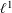
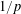

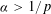
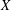
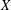
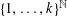
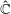
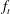
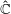
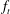
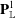

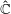
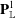
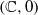
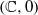
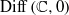
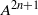
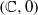
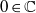
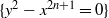
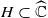 such that (1)
such that (1) 