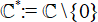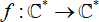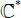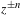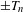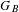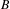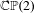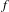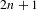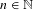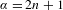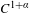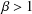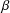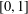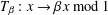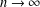Refine listing
Actions for selected content:
126 results in 37Fxx
Escaping Fatou components of transcendental self-maps of the punctured plane
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 28 November 2019, pp. 265-289
- Print publication:
- March 2021
-
- Article
- Export citation
Higher-dimensional foliated Mori theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 14 November 2019, pp. 1-38
- Print publication:
- January 2020
-
- Article
- Export citation
Entropy of transcendental entire functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 338-348
- Print publication:
- February 2021
-
- Article
- Export citation
The numbers of periodic orbits hidden at fixed points of holomorphic maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 578-592
- Print publication:
- February 2021
-
- Article
- Export citation
Commuting rational functions revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 August 2019, pp. 295-320
- Print publication:
- January 2021
-
- Article
- Export citation
Fatou components and singularities of meromorphic functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 633-654
- Print publication:
- April 2020
-
- Article
- Export citation
Dimension of ergodic measures and currents on
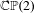 $\mathbb{C}\mathbb{P}(2)$
$\mathbb{C}\mathbb{P}(2)$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 04 January 2019, pp. 2131-2155
- Print publication:
- August 2020
-
- Article
- Export citation
Random local complex dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 2156-2182
- Print publication:
- August 2020
-
- Article
- Export citation
Dynamical degrees of Hurwitz correspondences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1968-1990
- Print publication:
- July 2020
-
- Article
- Export citation
Renormalization in the golden-mean semi-Siegel Hénon family: universality and non-rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 25 September 2018, pp. 1108-1152
- Print publication:
- April 2020
-
- Article
- Export citation
Rigidity, universality, and hyperbolicity of renormalization for critical circle maps with non-integer exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 25 September 2018, pp. 1282-1334
- Print publication:
- May 2020
-
- Article
- Export citation
DEGENERATION OF ENDOMORPHISMS OF THE COMPLEX PROJECTIVE SPACE IN THE HYBRID SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 31 August 2018, pp. 1141-1183
- Print publication:
- July 2020
-
- Article
- Export citation
Parametric rigidity of real families of conformal diffeomorphisms tangent to x→−x
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 261-277
- Print publication:
- February 2019
-
- Article
- Export citation
TWO-DIMENSIONAL SHRINKING TARGET PROBLEM IN BETA-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 33-42
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Homotopy linear algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 293-325
- Print publication:
- April 2018
-
- Article
- Export citation
CHARACTERIZATION OF PROJECTIVE SPACES AND
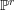 $\mathbb{P}^{r}$-BUNDLES AS AMPLE DIVISORS
$\mathbb{P}^{r}$-BUNDLES AS AMPLE DIVISORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 08 September 2017, pp. 155-169
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
Hyperbolic Metric and Multiply Connected Wandering Domains of Meromorphic Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 787-810
-
- Article
- Export citation
The Hausdorff Dimension is Convex on the Left Side of 1/4
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 911-936
-
- Article
- Export citation
CONTINUITY OF THE HAUSDORFF DIMENSION FOR GRAPH-DIRECTED SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 471-478
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
On Geodesics in Asymptotic Universal Teichmüller Space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 1065-1074
-
- Article
- Export citation