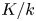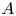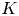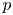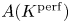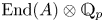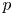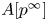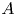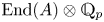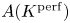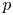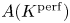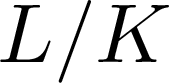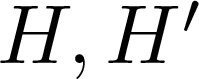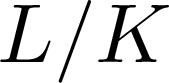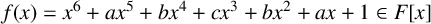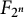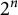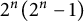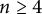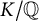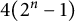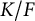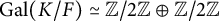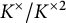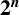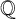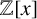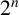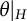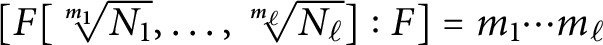Refine listing
Actions for selected content:
41 results in 12Fxx
AN EFFECTIVE VERSION OF THE PRIMITIVE ELEMENT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-8
-
- Article
- Export citation
Motivic versions of mass formulas by Krasner, Serre and Bhargava
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e148
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE TRIVIALITY OF AN
 $\mathbb A^2$-FIBRATION OVER A DVR
$\mathbb A^2$-FIBRATION OVER A DVR
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 12 September 2025, pp. 826-832
- Print publication:
- December 2025
-
- Article
- Export citation
Characterising local fields of positive characteristic by Galois theory and the Brauer group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 13 October 2025, pp. 2136-2153
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KRONECKER CLASSES, NORMAL COVERINGS AND CHIEF FACTORS OF GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GALOIS GROUPS OF POWER COMPOSITIONAL NONIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 458-472
- Print publication:
- December 2025
-
- Article
- Export citation
NORMAL BASES FOR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 44-55
- Print publication:
- August 2024
-
- Article
- Export citation
The tamely ramified geometric quantitative minimal ramification problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 21-51
- Print publication:
- January 2024
-
- Article
- Export citation
Perfect points of abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. 2261-2278
- Print publication:
- November 2023
-
- Article
- Export citation
On ρ-conjugate Hopf–Galois structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 288-304
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GALOIS GROUPS OF RECIPROCAL SEXTIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 37-44
- Print publication:
- February 2024
-
- Article
- Export citation
Modular forms and some cases of the Inverse Galois Problem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 568-586
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmetically equivalent fields in a Galois extension with Frobenius Galois group of 2-power degree
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 June 2022, pp. 380-394
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois module structure of square power classes for biquadratic extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 804-827
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RECIPROCAL MONOGENIC QUINTINOMIALS OF DEGREE
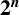 $\boldsymbol {2^n}$
$\boldsymbol {2^n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 437-447
- Print publication:
- December 2022
-
- Article
- Export citation
THE p-ZASSENHAUS FILTRATION OF A FREE PROFINITE GROUP AND SHUFFLE RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 961-983
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois-theoretic features for 1-smooth pro-p groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 525-541
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the degree of repeated radical extensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 23 November 2020, pp. 877-885
- Print publication:
- December 2021
-
- Article
- Export citation
ON UNRAMIFIED SOLVABLE EXTENSIONS OF SMALL NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 428-437
- Print publication:
- June 2021
-
- Article
- Export citation
WILD RAMIFICATION IN TRINOMIAL EXTENSIONS AND GALOIS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 106-120
- Print publication:
- January 2021
-
- Article
- Export citation