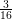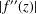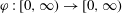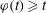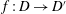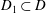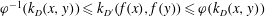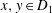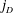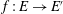Refine listing
Actions for selected content:
81 results in 30Fxx
On Selberg’s eigenvalue conjecture for moduli spaces of abelian differentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 30 October 2019, pp. 2354-2398
- Print publication:
- December 2019
-
- Article
- Export citation
Green Function and Self-adjoint Laplacians on Polyhedral Surfaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 02 July 2019, pp. 1324-1351
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
ESTIMATES OF THE SECOND DERIVATIVE OF BOUNDED ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 03 June 2019, pp. 458-469
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Local-global principles in circle packings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1118-1170
- Print publication:
- June 2019
-
- Article
- Export citation
ON ODD-DIMENSIONAL COMPLEX ANALYTIC KLEINIAN GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 12 February 2019, pp. 1-32
-
- Article
-
- You have access
- Export citation
Persistent Hall rays for Lagrange spectra at cusps of Riemann surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 2017-2072
- Print publication:
- August 2020
-
- Article
- Export citation
Determinant of the Laplacian on Tori of Constant Positive Curvature with one Conical Point
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 341-347
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Manhattan curves for hyperbolic surfaces with cusps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1843-1874
- Print publication:
- July 2020
-
- Article
- Export citation
A STRUCTURED DESCRIPTION OF THE GENUS SPECTRUM OF ABELIAN p-GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 10 July 2018, pp. 381-423
-
- Article
-
- You have access
- Export citation
MAPPING PROPERTIES OF A SCALE INVARIANT CASSINIAN METRIC AND A GROMOV HYPERBOLIC METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 18 August 2017, pp. 141-152
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
SYMMETRIC CROSSCAP NUMBER OF GROUPS OF ORDER LESS THAN OR EQUAL TO 63
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 145-156
-
- Article
-
- You have access
- Export citation
POLYGONAL QUASICONFORMAL MAPPINGS AND CHORD-ARC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 66-72
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
NONDECREASABLE AND WEAKLY NONDECREASABLE DILATATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 420-434
-
- Article
-
- You have access
- Export citation
A TOWER OF RIEMANN SURFACES WHICH CANNOT BE DEFINED OVER THEIR FIELD OF MODULI
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 379-393
-
- Article
-
- You have access
- Export citation
MODULI SPACES OF SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 10 April 2015, pp. 168-170
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
ON THE CONNECTEDNESS OF THE BRANCH LOCI OF NON-ORIENTABLE UNBORDERED KLEIN SURFACES OF LOW GENUS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 211-230
-
- Article
-
- You have access
- Export citation
Products of twists, geodesic lengths and Thurston shears
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 313-350
- Print publication:
- February 2015
-
- Article
- Export citation
FREELY QUASICONFORMAL MAPS AND DISTANCE RATIO METRIC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 383-390
-
- Article
-
- You have access
- Export citation
Numerical calculation of three-point branched covers of the projective line
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 379-430
-
- Article
-
- You have access
- Export citation
EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 14 May 2014, pp. 257-306
- Print publication:
- July 2014
-
- Article
- Export citation